Statistical Hypothesis Testing

STAT 120

Bastola

Introduction to Hypothesis Tests

Two Competing Hypotheses:

  1. Null Hypothesis \((H_0)\): Assumes no effect or no difference.
  2. Alternative Hypothesis \((H_a)\): Suggests a specific effect or difference exists.

  • Specifying Hypotheses: We frame these hypotheses in terms of population parameters (like mean, proportion, etc.).

  • Example:

    • \(H_0\): The mean weight of fish = 3 pounds.
    • \(H_a\): The mean weight of fish ≠ 3 pounds.

Our goal is to determine which hypothesis is more likely given our sample data.

Another Motivating Example: Extrasensory Perception


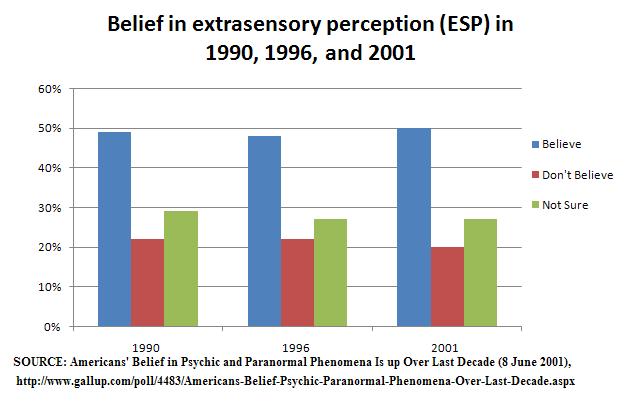
Source: click here

Extrasensory Perception



Subjects draw a card at random and telepathically communicate this to someone who then guesses the symbol

 Group Activity 1



10:00

Suppose you did this 10 times and guessed correctly 3 times. Is this evidence that you have ESP abilities?

Extrasensory Perception

There are five cards with five different symbols. If there is no such thing as ESP, what proportion p of guesses should be correct?

  1. \(\mathrm{p}=0\)
  2. \(\mathrm{p}=1/ 4\)
  3. \(\mathrm{p}=1 / 5\)
  4. \(\mathrm{p}=1 / 2\)
Click for answer The correct answer is 3. (since there are five choices and we are randomly guessing)

Extrasensory Perception

Let \(\hat{p}\) denote the sample proportion of correct guesses. Which of the statistics below would give the strongest evidence for ESP?

  1. \(\hat{\mathrm{p}}=0\)
  2. \(\hat{\mathrm{p}}=1 / 5\)
  3. \(\hat{\mathrm{p}}=1 / 2\)
  4. \(\hat{\mathrm{p}}=3 / 4\)
Click for answer The correct answer is 4. Since more correct means ESP.

Hypothesis Testing: A Recap

  • Goal: Use sample data to assess population claims.
  • Null Hypothesis \((H_0)\): No effect or difference.
  • Alternative Hypothesis \((H_a)\): Evidence-seeking claim.
  • Tests reveal if observed stats suggest genuine difference or result from random chance.
  • Aim: Refute \(H_0\) with enough evidence.

Extrasensory Perception

  • As we’ve learned, statistics vary from sample to sample
  • Even if the “population/true” proportion is \(\mathrm{p}=1/5\), not every sample proportion will be exactly \(1/5\)

How do we determine when a sample proportion is far enough above 1/5 to provide evidence of ESP?

ESP Hypothesis

For the ESP experiment:

  • \(\mathrm{H}_{0}: \mathrm{p}=1 / 5\)
  • \(\mathrm{H}_{\mathrm{a}}: \mathrm{p}>1 / 5\)

Helpful hints

  • \(\mathrm{H}_{0}\) usually includes \(=\)
  • \(\mathrm{H}_{\mathrm{a}}\) usually includes \(>,<\), or \(\neq\)
  • The direction in \(\mathrm{H}_{\mathrm{a}}\) depends on the question being asked, not based on what the data shows!

Moving Forward…

How to test if observed difference between groups is real or just due to random chance?

Sleep Vs. Caffeine

Students were given words to memorize, then randomly assigned to take either a 90 min nap, or a caffeine pill. \(2 \frac{1}{2}\) hours later, they were tested on their recall ability.

  • Explanatory variable: sleep or caffeine
  • Response variable: number of words recalled

Research Question: Is sleep or caffeine better for memory?

Mednick, Cai, Kanady, and Drummond (2008). “Comparing the benefits of caffeine, naps and placebo on verbal, motor and perceptual memory,” Behavioral Brain Research, 193, 79-86.

Sleep Vs. Caffeine

What is the parameter of interest in the sleep versus caffeine experiment?

  1. Proportion
  2. Difference in proportions
  3. Mean
  4. Difference in means
  5. Correlation
Click for answer

The correct answer is 4.

Difference in mean responses \(\mu_1 - \mu_2\), where \(\mu_1\) and \(\mu_2\) are the mean words recalled in the two different conditions

Sleep Vs. Caffeine

Let \(\mu_{\mathrm{s}}\) and \(\mu_{\mathrm{c}}\) be the mean number of words recalled after sleeping and after caffeine.

  • Is there a difference in average word recall between sleep and caffeine?

Sleep Vs. Caffeine

What are the null and alternative hypothesis?

  1. \(\mathrm{H}_{0}: \mu_{\mathrm{s}} \neq \mu_{\mathrm{c}}, \mathrm{H}_{\mathrm{a}}: \mu_{\mathrm{s}}=\mu_{\mathrm{c}}\)
  2. \(\mathrm{H}_{0}: \mu_{\mathrm{s}}=\mu_{\mathrm{c}}, \mathrm{H}_{\mathrm{a}}: \mu_{\mathrm{s}} \neq \mu_{\mathrm{c}}\)
  3. \(\mathrm{H}_{0}: \mu_{\mathrm{s}} \neq \mu_{\mathrm{c}}, \mathrm{H}_{\mathrm{a}}: \mu_{\mathrm{s}}>\mu_{\mathrm{c}}\)
  4. \(\mathrm{H}_{0}: \mu_{\mathrm{s}}=\mu_{\mathrm{c}}, \mathrm{H}_{\mathrm{a}}: \mu_{\mathrm{s}}>\mu_{\mathrm{c}}\)
  5. \(\mathrm{H}_{0}: \mu_{\mathrm{s}}=\mu_{\mathrm{c}}, \mathrm{H}_{\mathrm{a}}: \mu_{\mathrm{s}}<\mu_{\mathrm{c}}\)
Click for answer The correct answer is 2 (since we are looking for evidence that the means are different)

Random chance using Statkey

How can we be sure if an observed difference between two groups is real, or if it’s just something that could happen by random chance?


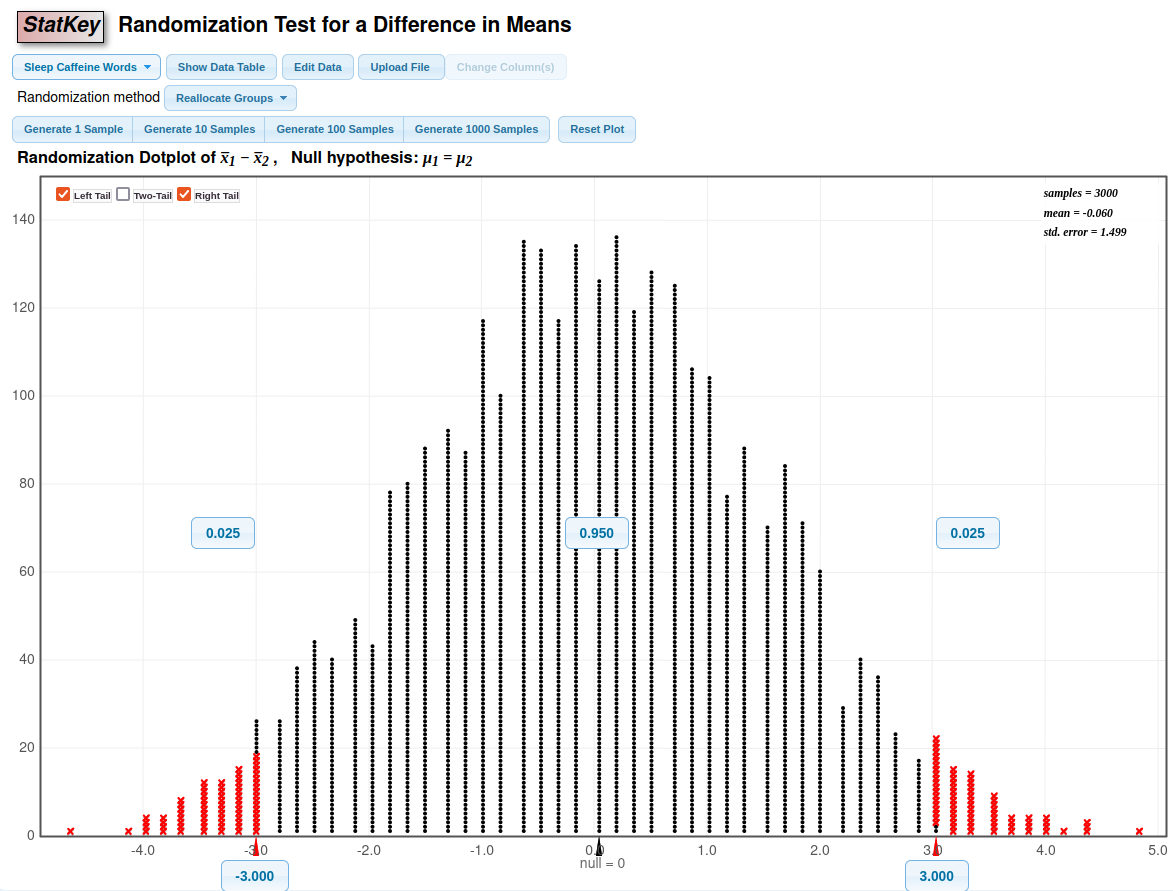
 Group Activity 2


  • Finish the rest of the class activity and submit to moodle when done.

20:00