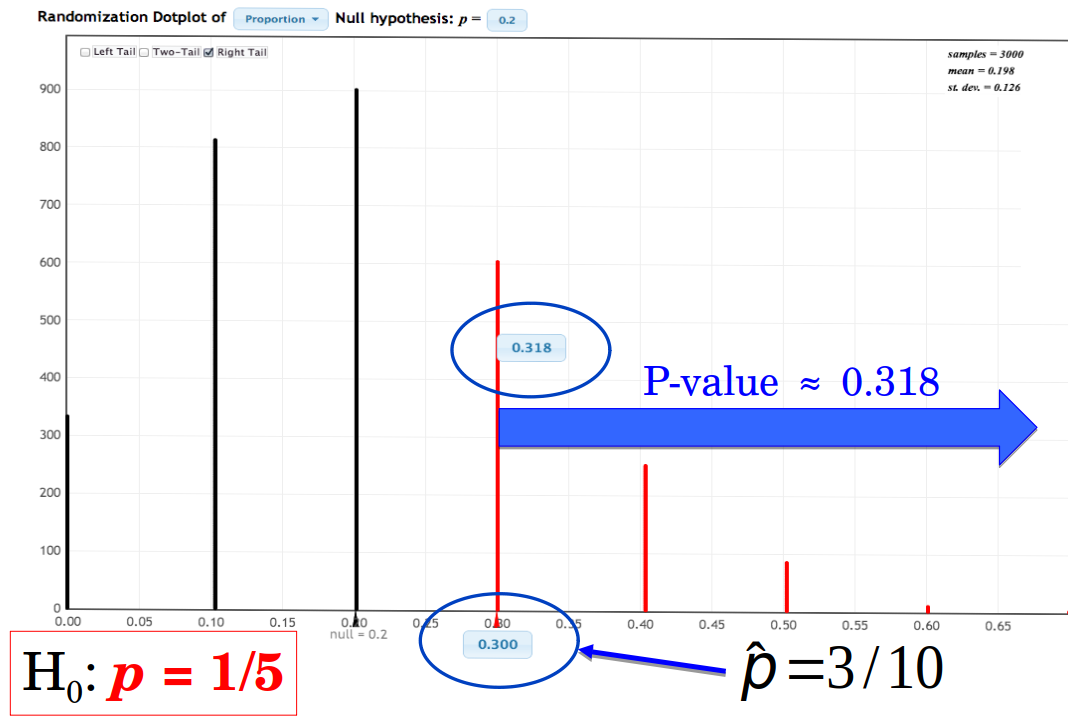
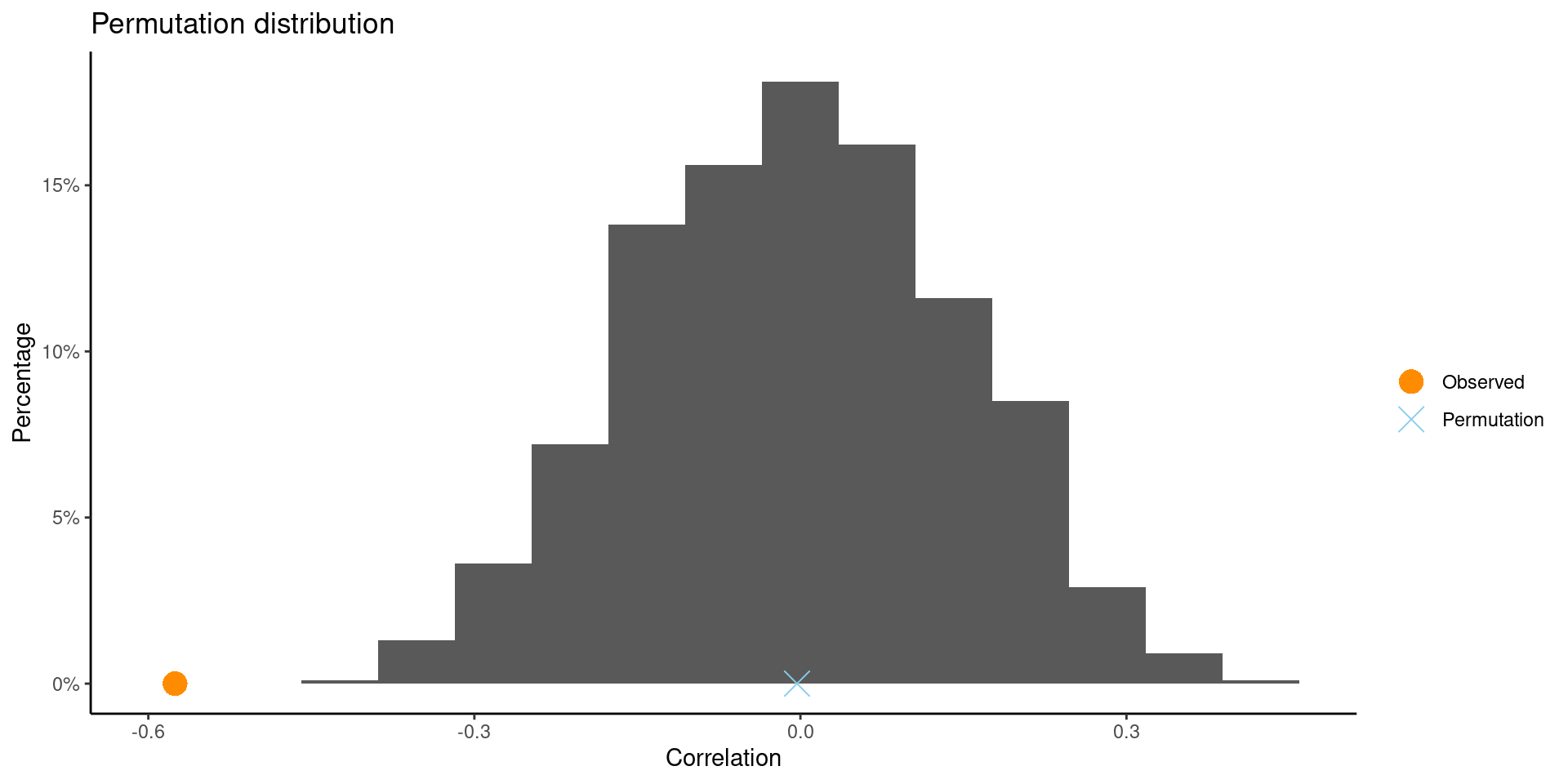
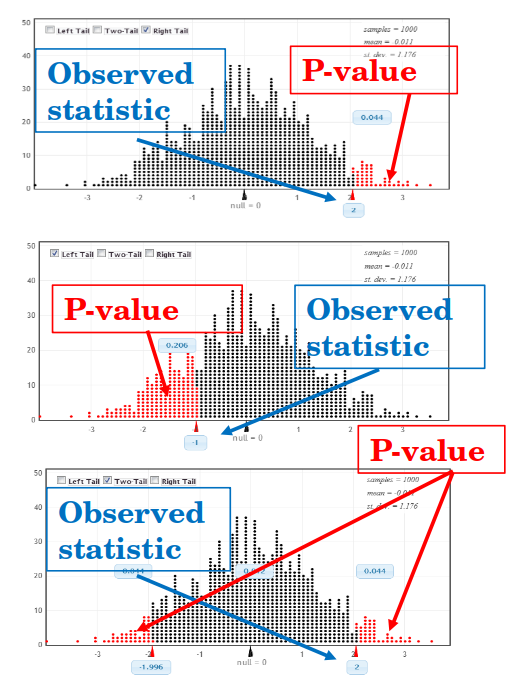
library(CarletonStats)
FloridaLakes <- read.csv("https://www.lock5stat.com/datasets2e/FloridaLakes.csv")
permTestCor(FloridaLakes$pH, FloridaLakes$AvgMercury)
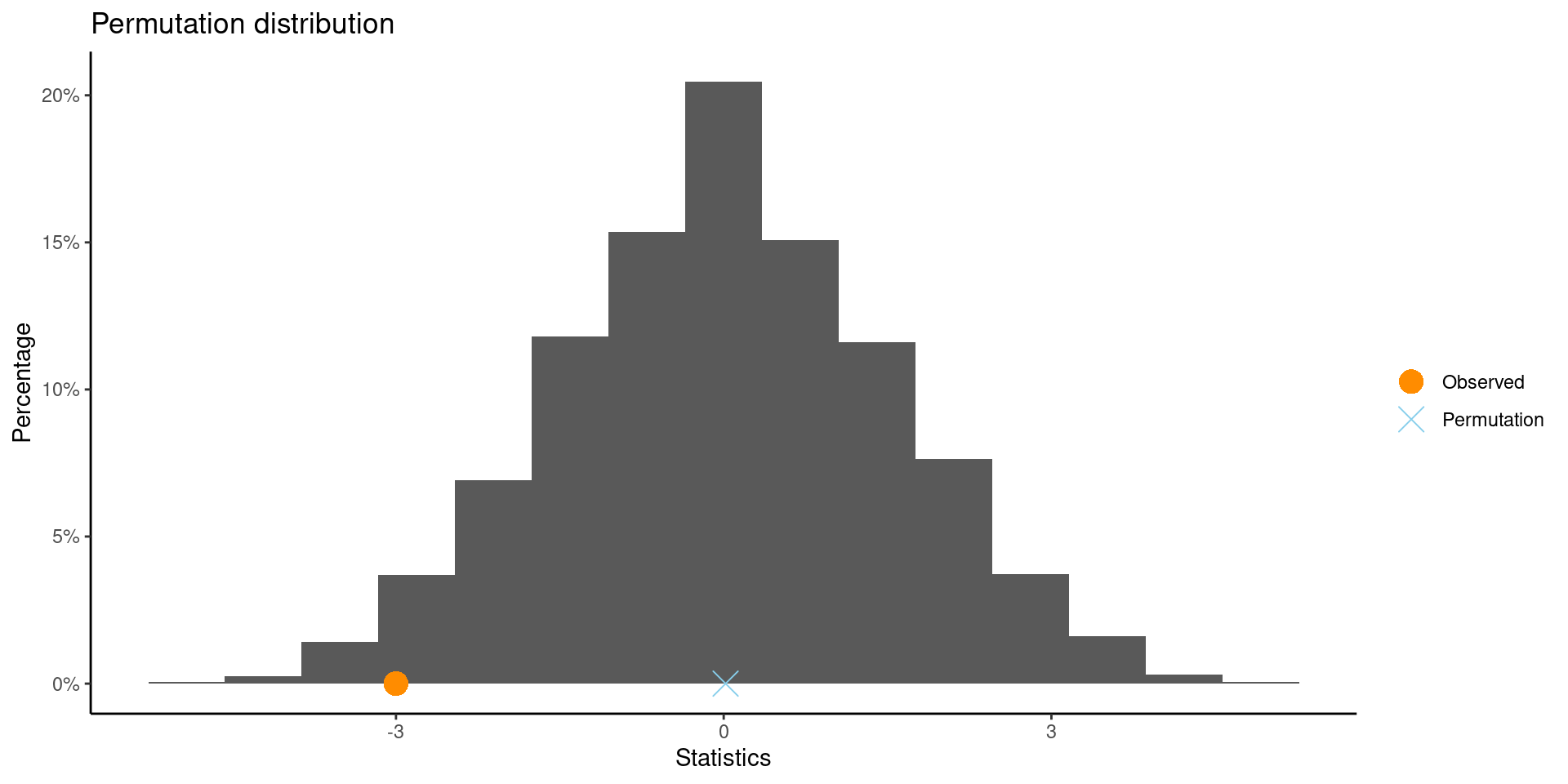
** Permutation test **
Permutation test with alternative: two.sided
Observed correlation between FloridaLakes$pH , FloridaLakes$AvgMercury : -0.5754
Mean of permutation distribution: -0.00314
Standard error of permutation distribution: 0.14681
P-value: 0.001
*-------------*