Hypothesis Testing: Significance

STAT 120

Bastola

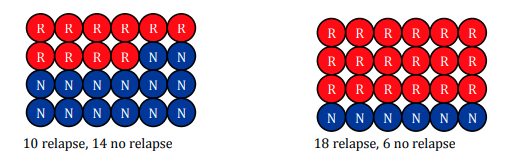
Recap: Coccaine Addiction

  Relapse No Relapse total
Desipramine 10 14 24
Lithium 18 6 24

Desipramine

Lithium

Recap: Randomization Distribution

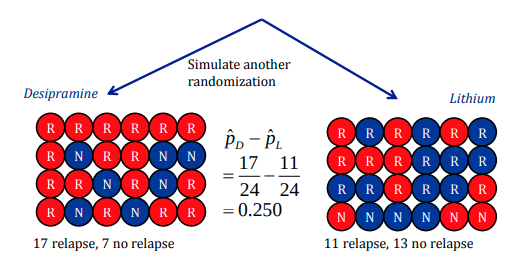
  • In the experiment, 28 people relapsed and 20 people did not relapse. Create cards or slips of paper with 28 “R” values and 20 “N” values.
  • Pool these response values together, and randomly divide them into two groups (representing Desipramine and Lithium)
  • Calculate your difference in proportions
  • Plot your statistic on a dotplot like how Statkey does
  • To create an entire randomization distribution, we simulate this process many more times with technology

Randomization 1



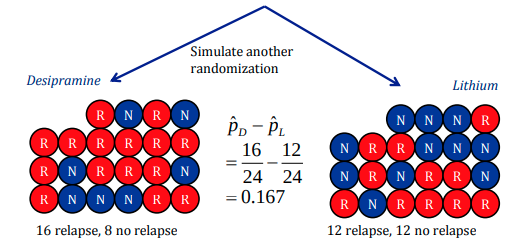
Randomization 2



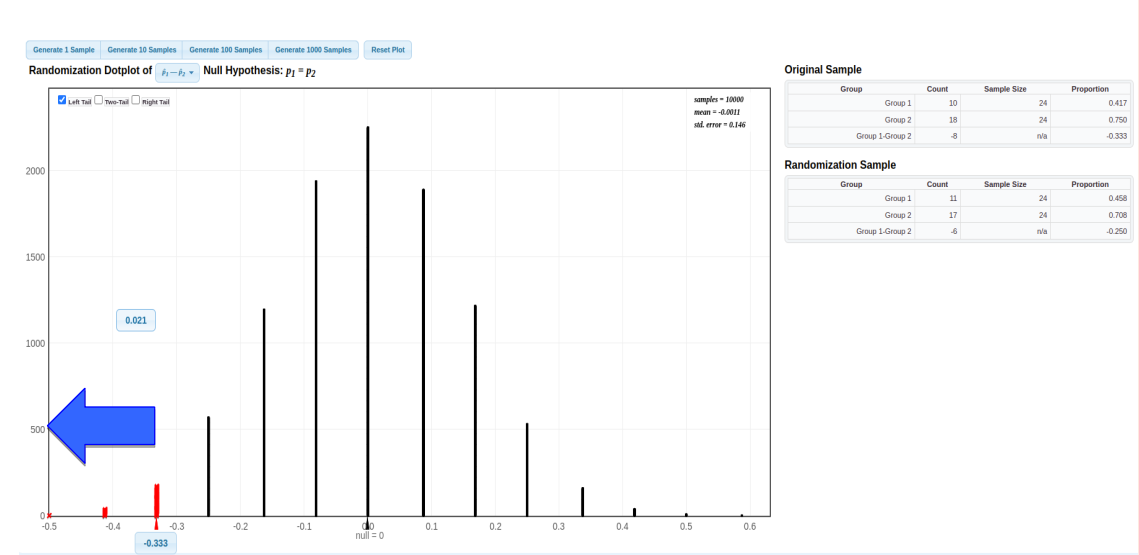
Randomization: Statkey


Formal Decisions

If the p-value is small:

  • REJECT \(\mathrm{H}_0\)
  • the sample would be extreme if \(\mathrm{H}_0\) were true
  • the results are statistically discernible
  • we have evidence for \(\mathrm{H}_{\mathrm{a}}\)

If the p-value is not small:

  • DO NOT REJECT \(\mathrm{H}_0\)
  • the sample would not be too extreme if \(\mathrm{H}_0\) were true
  • the results are not statistically discernible
  • the test is inconclusive; either \(\mathrm{H}_0\) or \(\mathrm{H}_{\mathrm{a}}\) may be true

Significance Level \(\&\) Formal Decisions

The significance level, \(\alpha\) is the threshold below which the p-value is deemed small enough to reject the null hypothesis (evidence is statistically discernible).

\[ \mathrm{p} \text {-value }<\alpha \quad \Longrightarrow \quad \text { Reject } \mathrm{H}_0 \] \[\mathrm{p} \text {-value } \geq \alpha \quad \Longrightarrow \text { Do not Reject } \mathrm{H}_0\] Common levels:

  • \(10 \%\) : need some evidence to reject the null
  • \(5 \%\) : need moderate evidence to reject the null
  • \(1 \%\) : need strong evidence to reject the null

Statistical Conclusions

Formal decision of hypothesis test, based on \(\alpha = 0.05\) :


Informal strength of evidence against H0:


Never Accept \(\mathrm{H}_0\)

For the logical fallacy of believing that 
a hypothesis has been proved to be true, 
merely because it is not contradicted by 
the available facts, has no more right 
to insinuate itself in statistical than 
in other kinds of scientific reasoning …”

Sir R. A. Fisher


“Do not reject \(\mathrm{H}_0\)” is not the same as “accept \(\mathrm{H}_0\)”! Lack of evidence against \(\mathrm{H}_0\) is NOT the same as evidence for \(\mathrm{H}_0\) !

Errors in Hypothesis Testing

Reject \(H_0\) Do not reject \(H_0\)
\(H_0\) true TYPE I ERROR 😀
\(H_0\) false 😀 TYPE II ERROR


  • A Type I Error is rejecting a true null (false positive)
  • A Type II Error is not rejecting a false null (false negative)

Analogy to law

Types of mistakes in a verdict?

\[\begin{align*} \text{Convict an innocent} &\Rightarrow \text{Type I error} \\ \text{Release a guilty} &\Rightarrow \text{Type II error} \end{align*}\]

\(\alpha=\) Probability of Type I Error

The significance level \(\alpha\) controls the type I error rate.

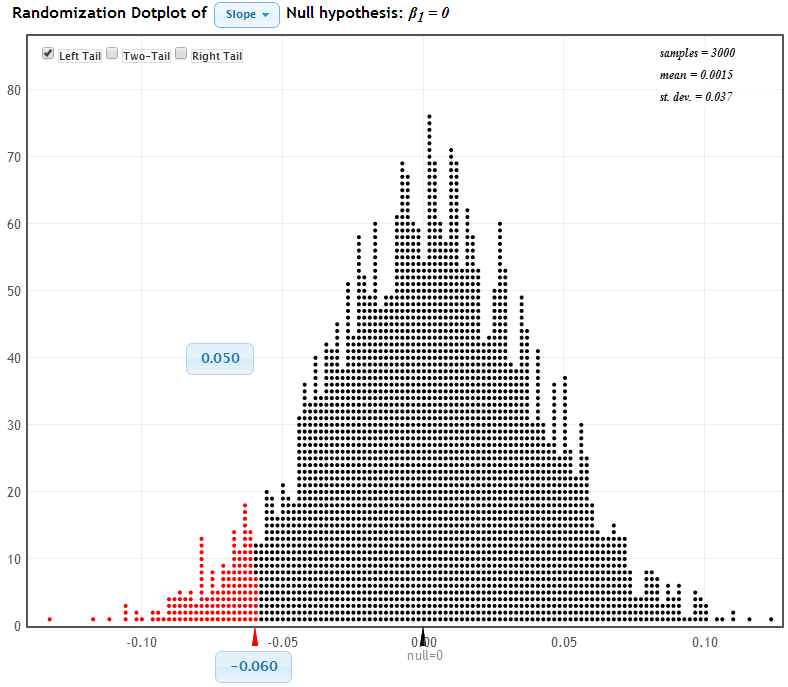
  • Recall the Florida Lakes slope test: \[\mathrm{H}_0: \beta=0 \quad \mathrm{H}_{\mathrm{a}}: \beta<0\]
  • If \(\mathrm{H}_0\) is true and \(\alpha=0.05\), then \(5 \%\) of sample slopes will be lower red tail \((b \leq 0.06)\).
  • \(5 \%\) of the sample slopes will give \(p\)-values less than \(0.05\), so \(5 \%\) of statistics will lead to rejecting \(\mathrm{H}_0\) if it is true (Type I error)!!!

Randomization distribution

Selecting a significance level

Decreasing \(\alpha\) will lower your Type I error rate (makes it harder to reject the null)

  • but it will also increase your type II error rate (makes it harder to accept a true alternative)

Selecting a significance level

If a Type I error (rejecting a true null) is much worse than a Type II error, we may choose a smaller \(\alpha\), like \(\alpha=0.01\) (need lots of evidence to reject null).

  • E.g. sending an innocent person to jail

Selecting a significance level

If a Type II error (not rejecting a false null) is much worse than a Type I error, we may choose a larger \(\alpha\), like \(\alpha=0.10\)

  • E.g. a false negative test for a serious disease

 Group Activity 1


30:00