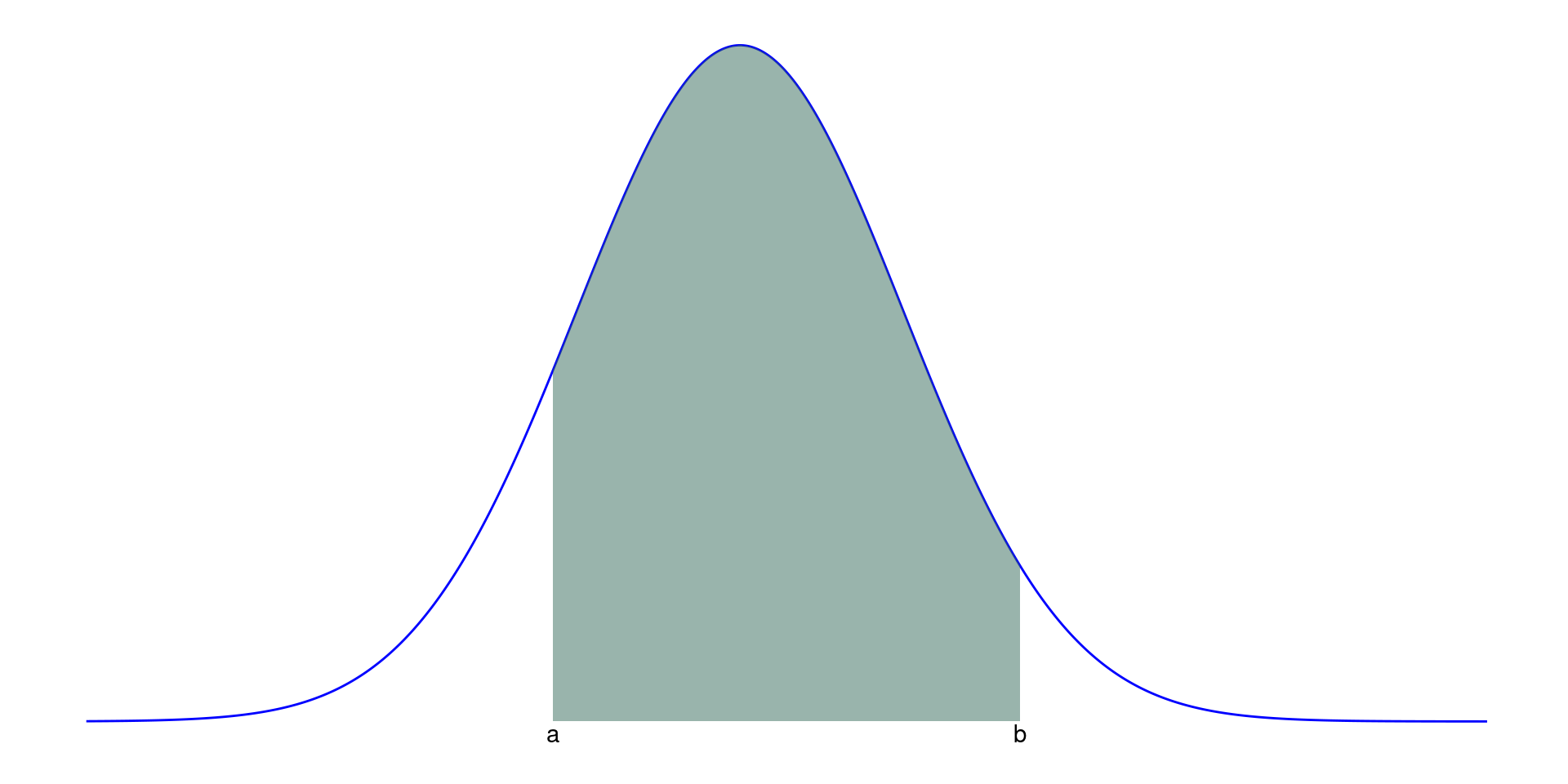
The Normal Distribution!
STAT 120
Bastola
Overview
Core intro stats covered: EDA for data comprehension, estimation with confidence, and hypothesis testing via p-values.
Upcoming focus: Advanced inference methods, transitioning from simulations to probability models for bootstrap/randomization distributions.
Density Curve
A density curve is a theoretical model to describe a distribution.
Distribution for
- individual measurements in population (for a quantitative variable)
- Sampling distribution for a statistic
All density curves have an area under the curve of 1 (100%)
- give proportions/percents as areas under the curve
Normal Distribution
A normal distribution has a symmetric bell-shaped density curve.
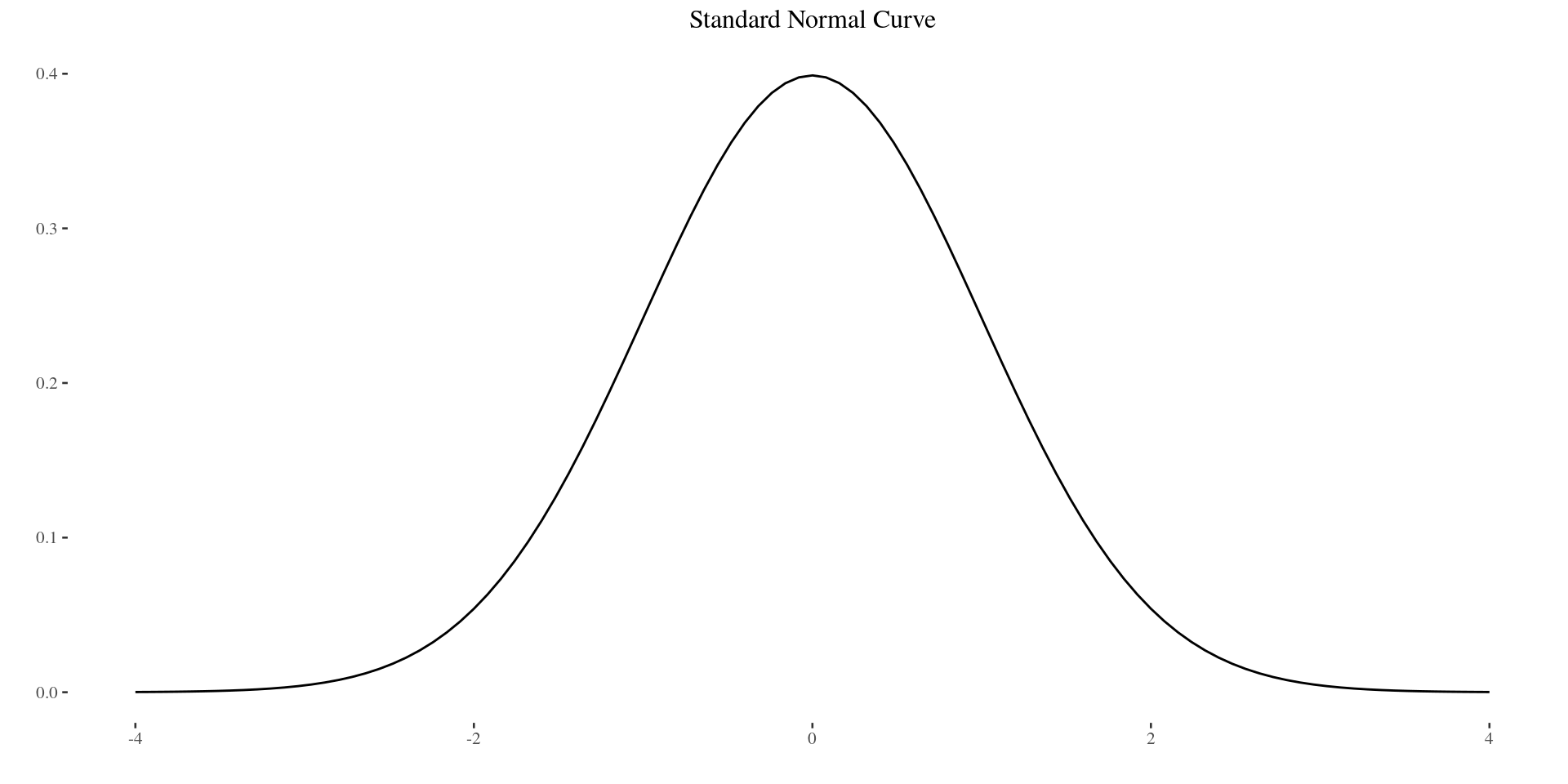
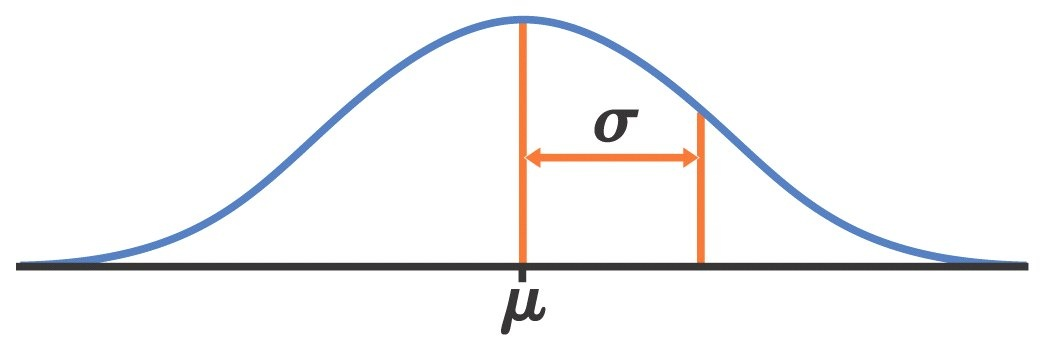
The Normal Model: \(X \sim N(\mu, \sigma)\)
The mean and SD determine how a normal density curve looks. The normal model parameters are
- \(\mu\) = model mean (center)
- \(\sigma=\) model SD (variability)
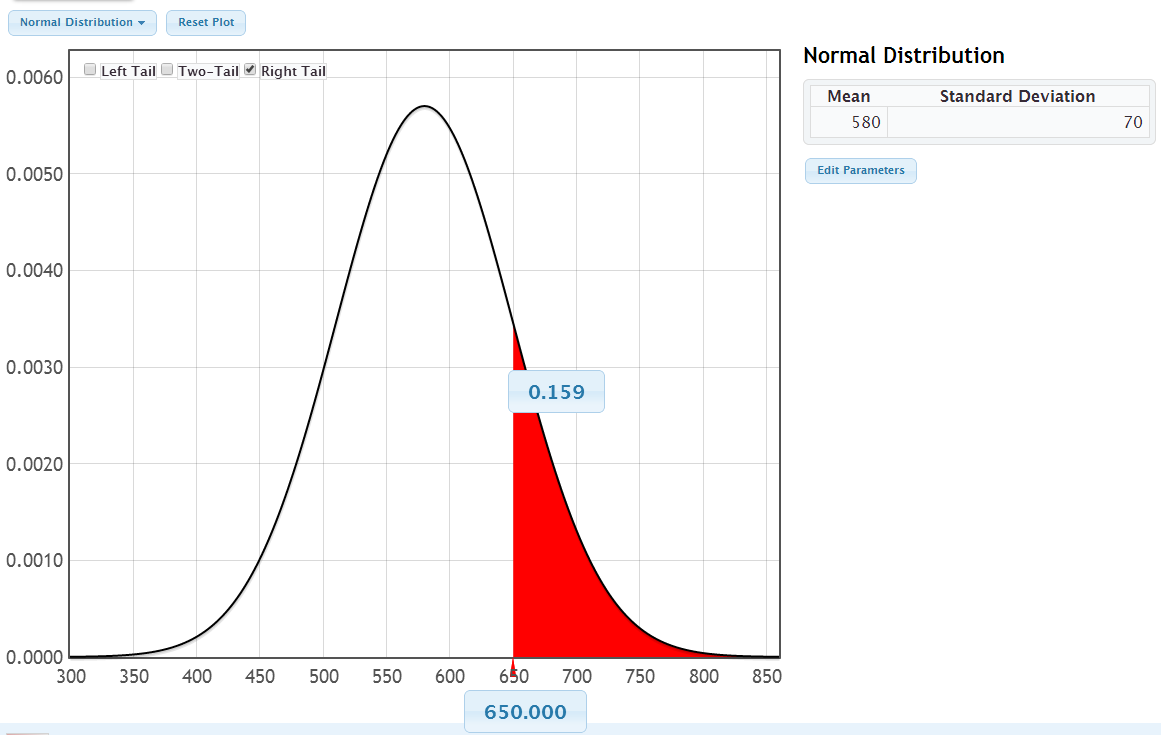
Verbal SAT \(\sim N(580,70)\)
What proportion of people score above 650?
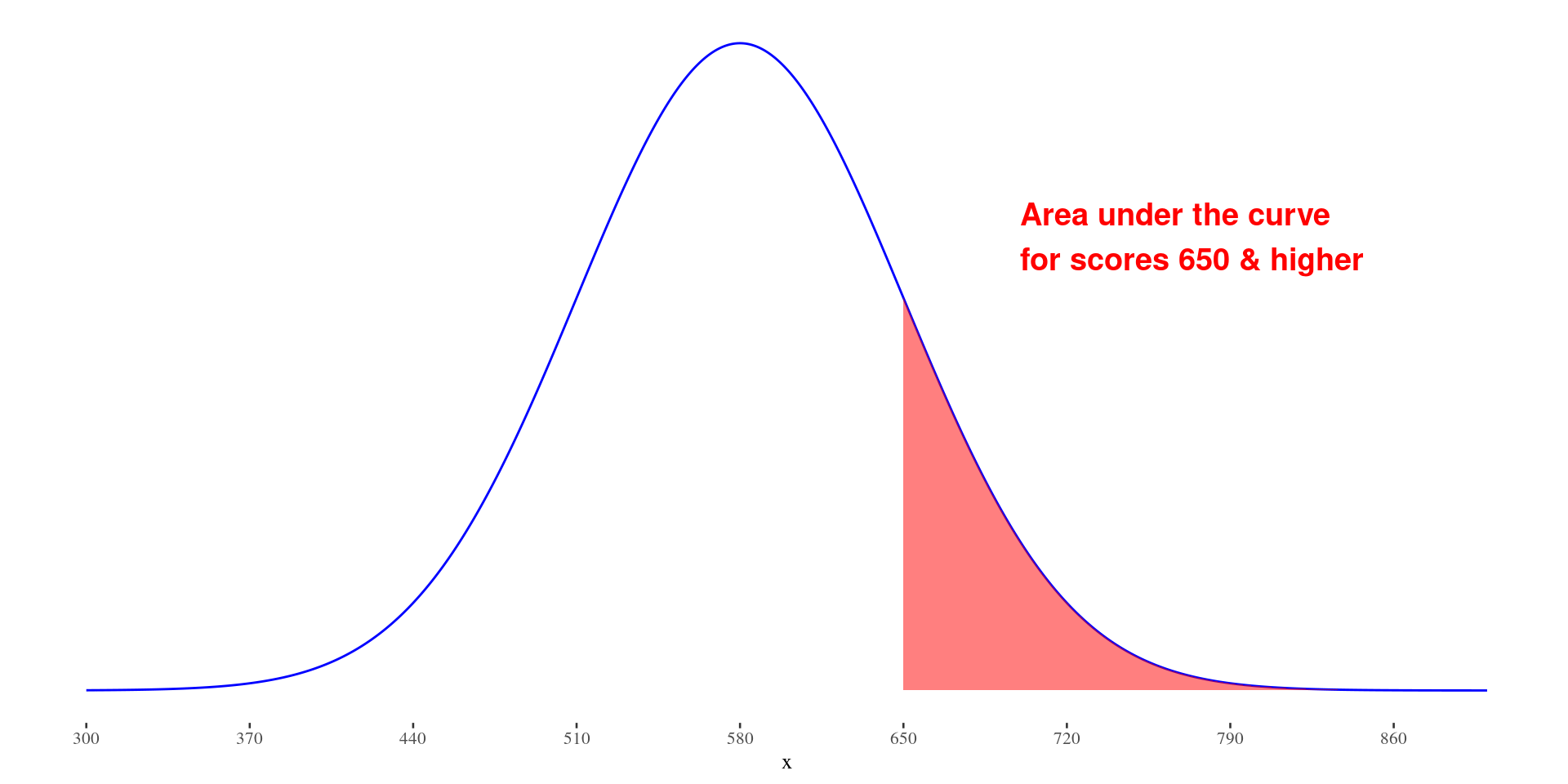
How can we find areas under a normal density?
- The curve represents the normal distribution, denoted by \(N(\mu, \sigma)\).
- (CALCULUS!!) Calculating the exact area requires integration, as given by the formula: Area \(=\int_a^b \frac{1}{\sqrt{2 \pi \sigma}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} d x\)
- We’ll just utilize technological tools.
StatKey – Verbal SAT: What proportion of people score above 650?
StatKey – Some observations 1
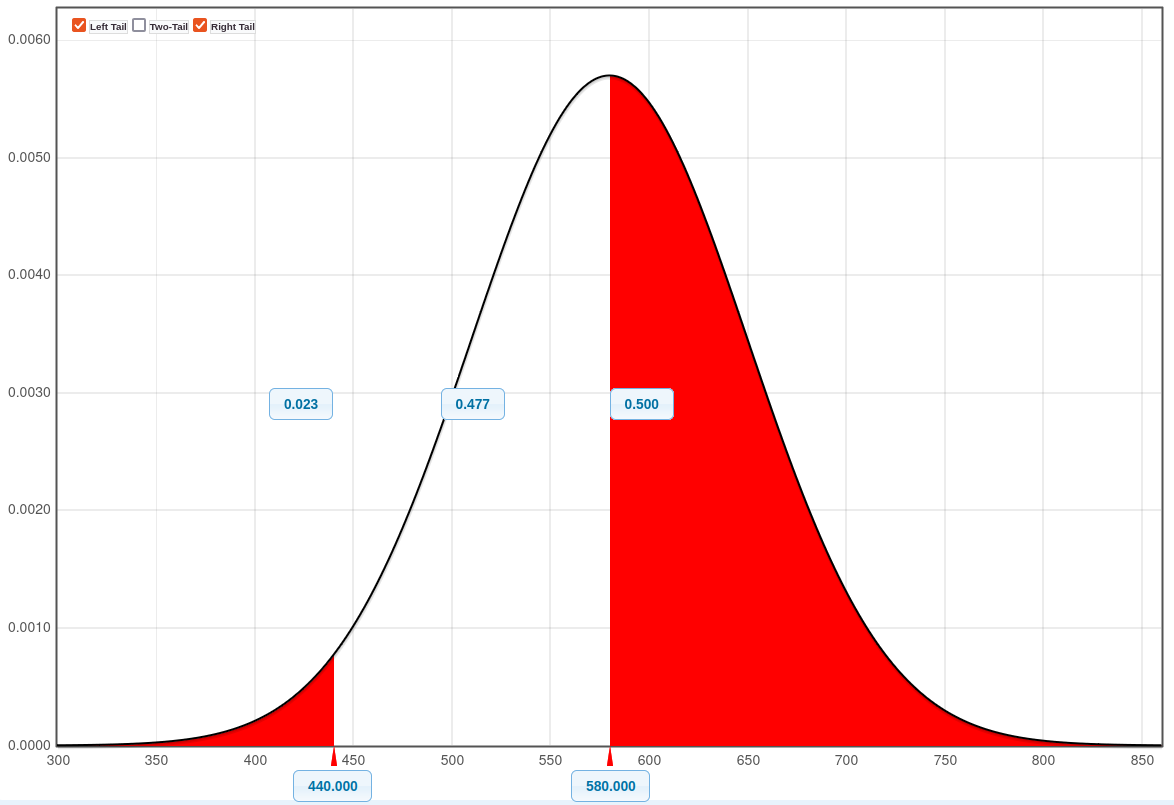
StatKey – Some observations 2
Example: Verbal SAT scores Using R
What percent of the population scored 650 or higher?
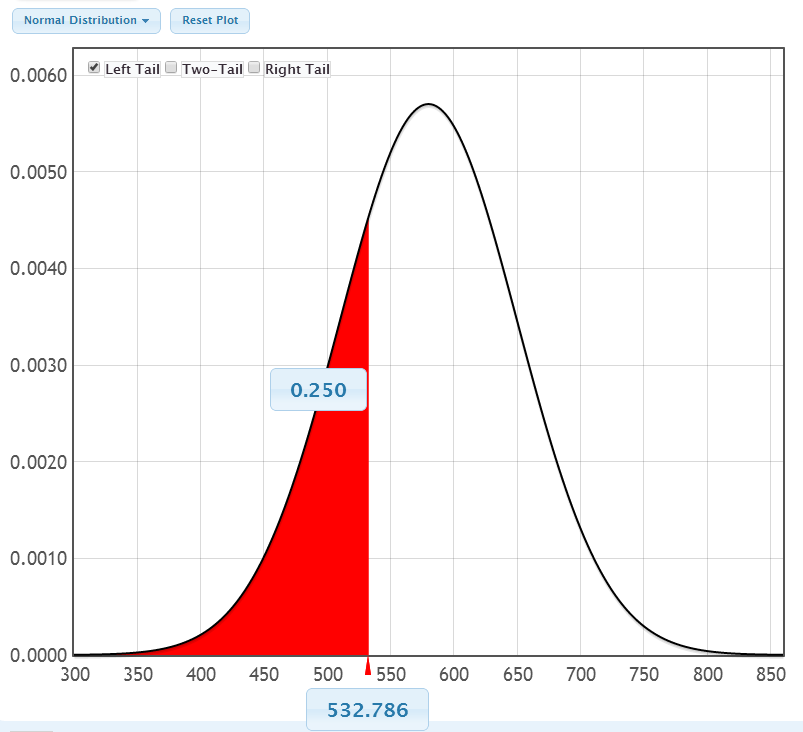
[1] 0.1586553[1] 0.1586553What score is the \(25^{th}\) percentile?
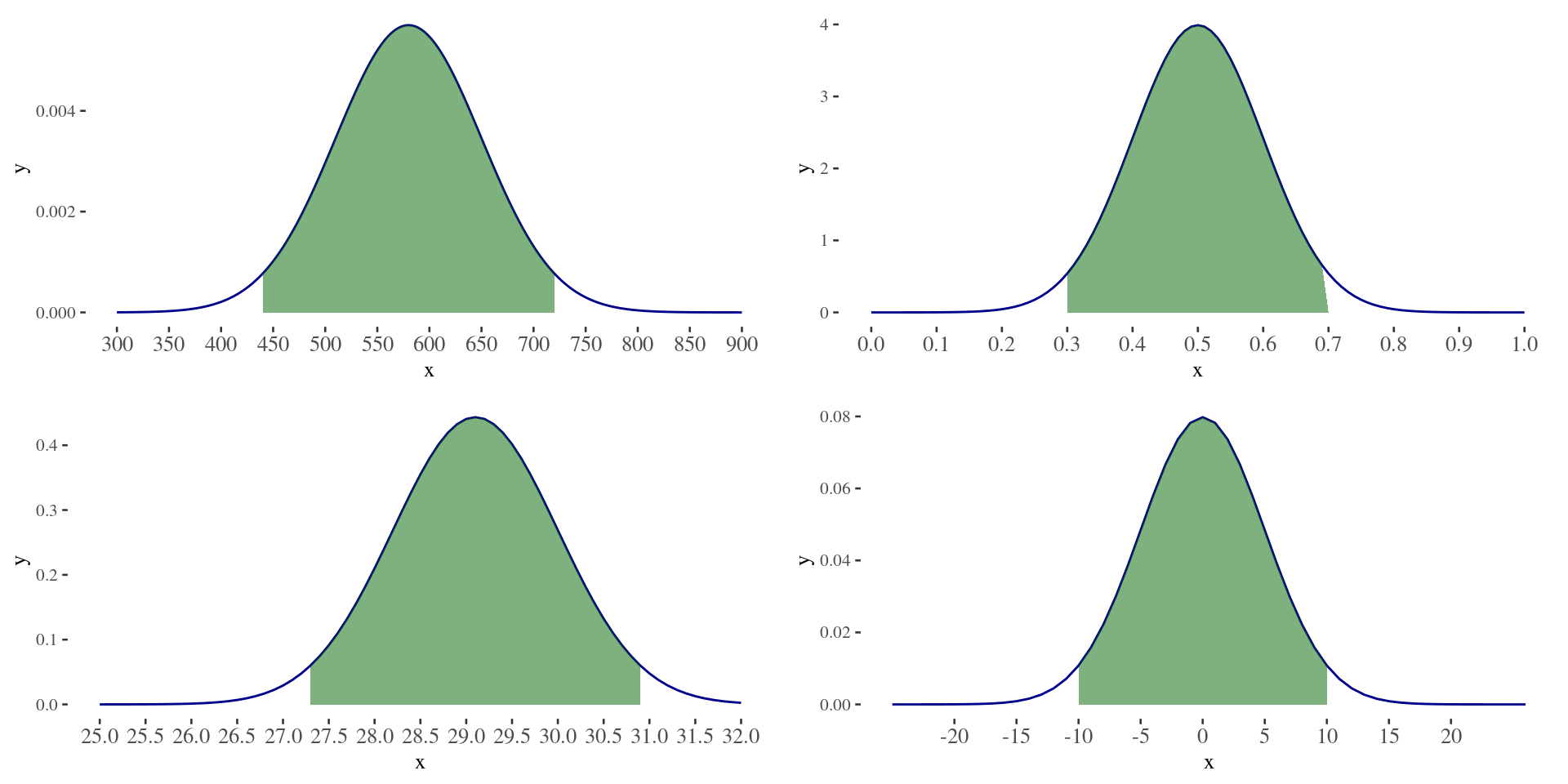
What is common in all 4 figures?
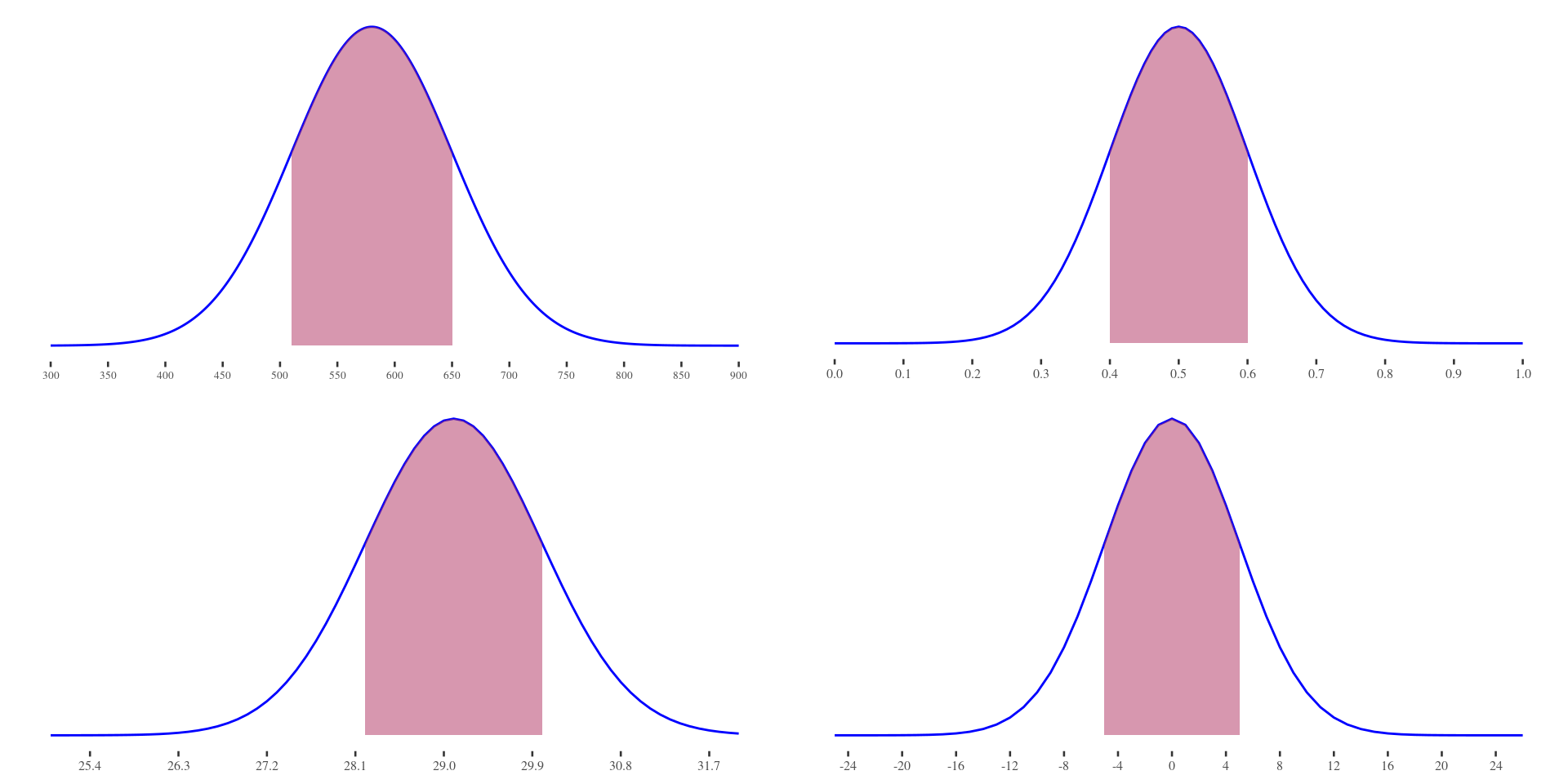
What is common in all these 4 figures?
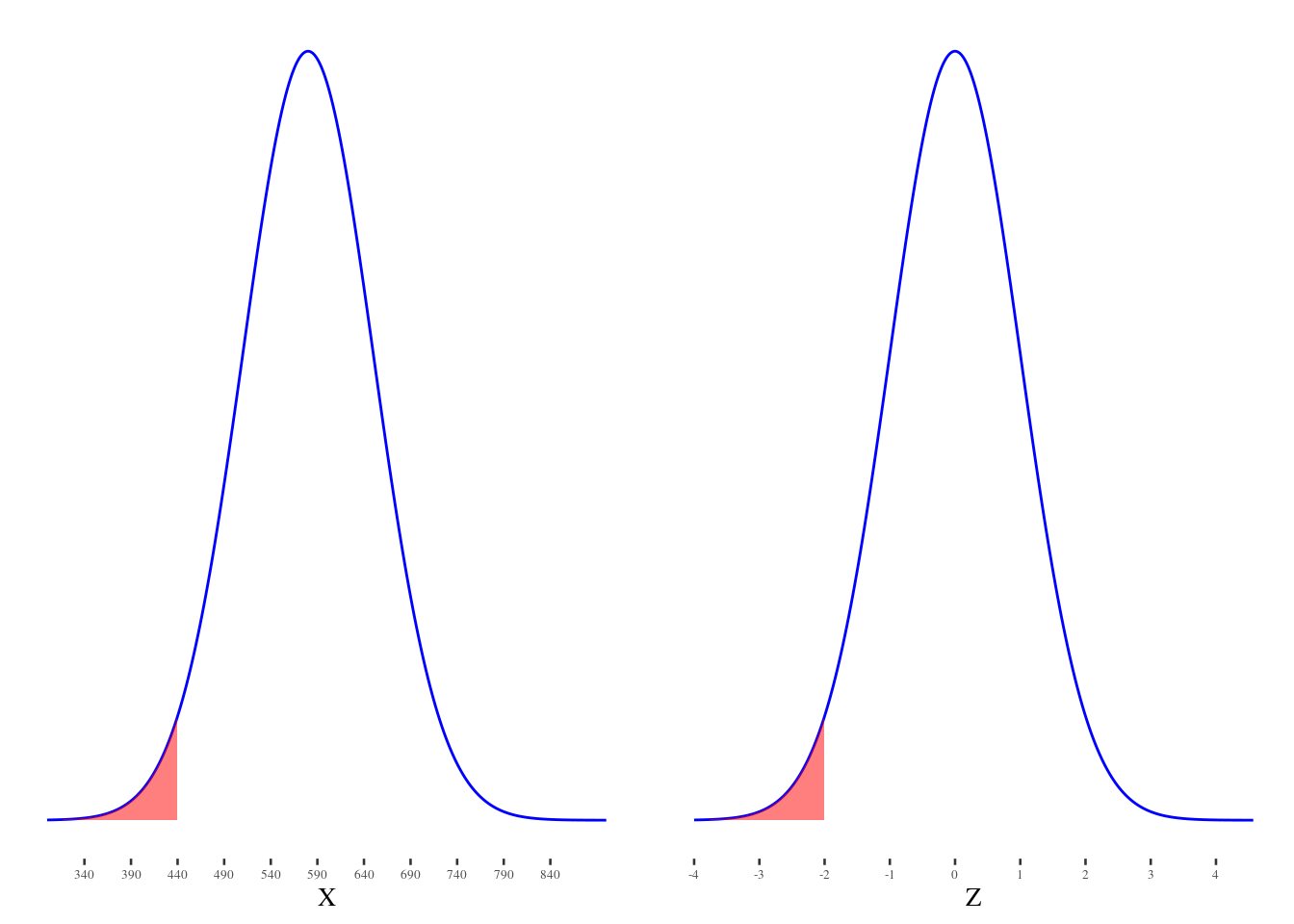
Connecting any Normal model to the standard normal model
Area below x = Area below z
Big picture
When have we already been using normal models??
- Bootstrap distributions – get confidence intervals if a bootstrap distribution is roughly bell-shaped
- Randomization distributions – many of these are bell-shaped.
- Normal models play a huge role in statistical inference.
- If we know the (bootstrap/randomization) standard error then we can just use a normal model rather than a resampling model (which requires more computational effort)
Group Activity 1

- Please download the Class-Activity-15 template from moodle and go to class helper web page
30:00