Hypothesis Tests and Confidence Intervals using Normal Distribution!

STAT 120

Bastola

How do Malaria parasites impact mosquito behavior?


Mosquitoes are tested with two mouse groups: Malaria-infected (experimental) and Healthy (control)

Stages of malaria in mice:

  • Stage 1: Non-infectious (Days 1-8)

  • Stage 2: Infectious (Days 9-28)

  • Response Variable: Whether the mosquito approaches a human.

Source

Research Hypothesis

Research Questions: Do mosquitoes behave differently around malaria-infected versus healthy mice? Does the infection stage affect their behavior?

Malaria parasites would benefit if

  • Mosquitoes approached humans less often after being exposed, but before becoming infectious, because humans are risky
  • Mosquitoes approached humans more often after becoming infectious, to pass on the infection

Days 1-8

We’ll first look at the mosquitoes before they become infectious (days 1-8).

\(p_C:\) proportion of controls to approach human

\(p_E:\) proportion of exposed to approach human

What are the relevant hypotheses?

A. \(\mathrm{H}_0: p_{\mathrm{E}}=p_{\mathrm{C}}, \mathrm{H}_{\mathrm{a}}: p_{\mathrm{E}}<p_{\mathrm{C}}\)

в. \(\mathrm{H}_0: p_{\mathrm{E}}=p_{\mathrm{C}}, \mathrm{H}_{\mathrm{a}}: p_{\mathrm{E}}>p_{\mathrm{C}}\)

  1. \(\mathrm{H}_0: p_{\mathrm{E}}<p_{\mathrm{C}}, \mathrm{H}_{\mathrm{a}}: p_{\mathrm{E}}=p_{\mathrm{C}}\)

D. \(H_0: p_{\mathrm{E}}>p_{\mathrm{C}}, \mathrm{H}_{\mathrm{a}}: p_{\mathrm{E}}=p_{\mathrm{C}}\)

Click for answer The correct answer is A. (since it favors parasites if exposed mosquitoes do not approach humans during this stage)

Sample data


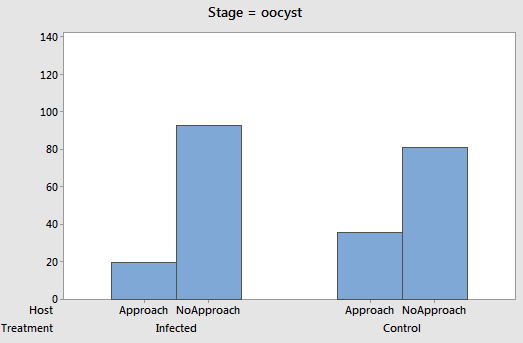
p̂E - p̂C = 20/113 - 36/117 = 0.177 - 0.308 = -0.131

Randomization Distribution


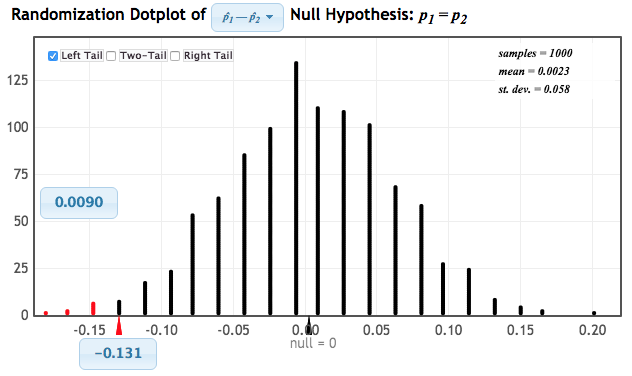
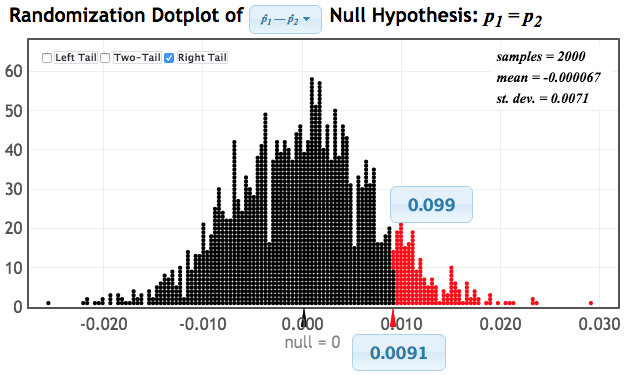
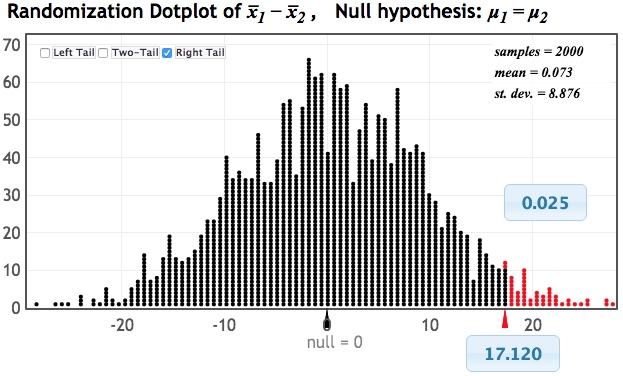
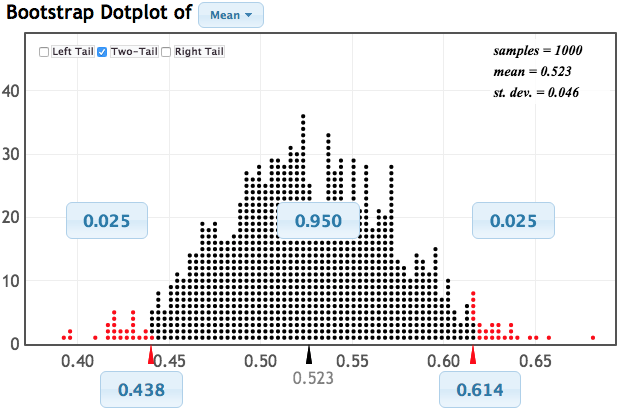
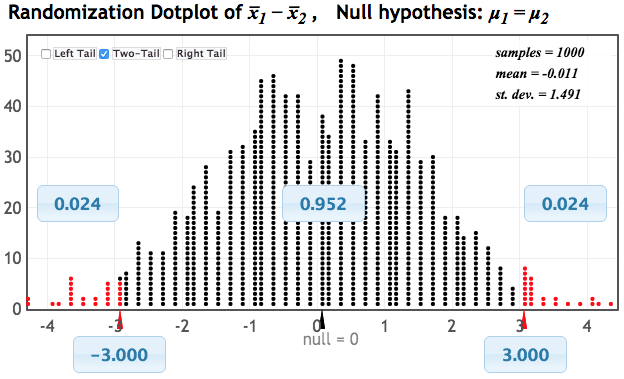
What do you notice?

Central Limit Theorem (CLT)

For random samples with a sufficiently large sample size, the distribution of sample statistics for a mean or a proportion is normally distributed

The catch: “sufficiently large sample size”

The more skewed the original distribution of data/population is, the larger \(n\) has to be for the CLT to work

  • For quantitative variables that are not very skewed, \(\boldsymbol{n} \geq \mathbf{3 0}\) is usually sufficient
  • For categorical variables, counts of at least 10 within each category is usually sufficient

Which normal distribution?


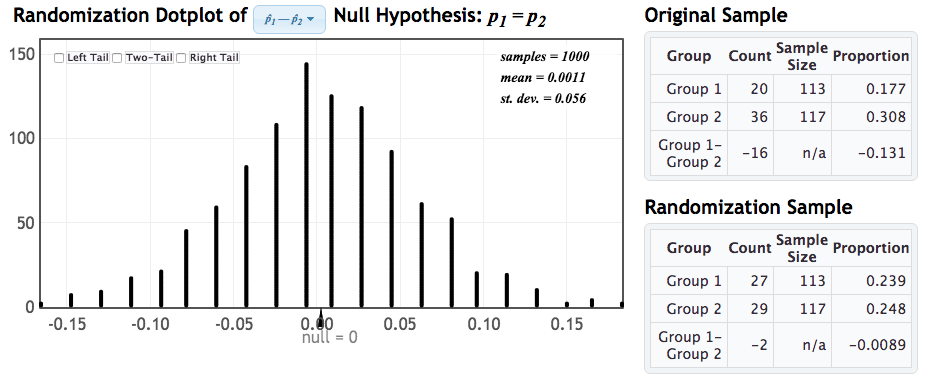
\[\begin{aligned} A. \quad & \mathrm{N}(0,-0.131) \\ B. \quad& \mathrm{N}(0,0.056) \\ C. \quad& \mathrm{N}(-0.131,0.056) \\ D. \quad& \mathrm{N}(0.056,0) \end{aligned}\]
Click for answer The correct answer is B. (since the distribution is centered at 0 and has standard deviation of 0.056)

Statkey: p-value from N(null, SE)

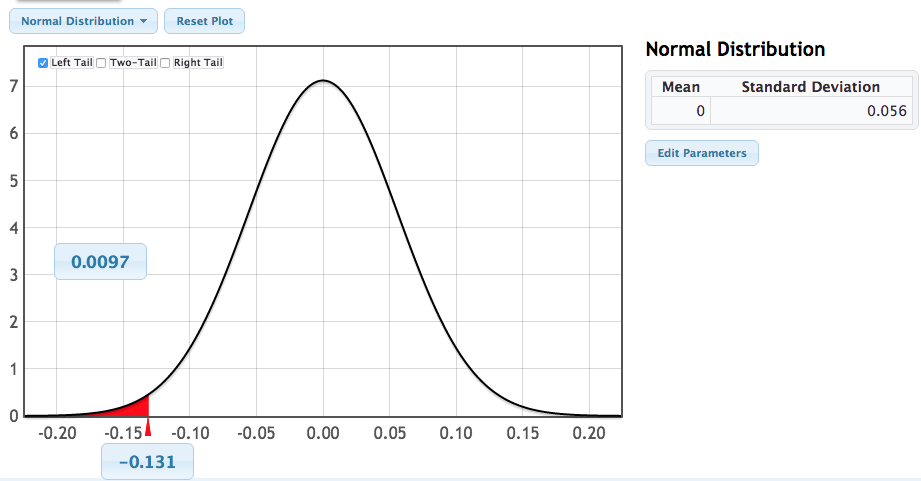
Connecting Normal model to hypothesis tests

Suppose: randomization distribution is bell shaped.

  • Center: hypothesized null parameter value
  • Spread: the standard error given in the randomization graph (or by formula)
  • P-value: computed from the normal model the “usual” way - the chance of being as extreme, or more extreme, than the observed statistic.

Standardized Statistic

The standardized test statistic (also known as a z-statistic) is \[\begin{align*} z=\frac{\text { statistic }-\text { null }}{S E} \end{align*}\]

Calculating the number of standard errors a statistic is from the null lets us assess extremity on a common scale.

Malaria and Mosquitos

Does infecting mosquitoes with Malaria actually impact the mosquitoes’ behavior to favor the parasite?

  • After the parasite becomes infectious, do infected mosquitoes approach humans more often, so as to pass on the infection?

Days 9 – 28

For the data after the mosquitoes become infectious (Days \(9-28\)), what are the relevant hypotheses?

\[\begin{align} \boldsymbol{p}_{C}: & \text{proportion of controls to approach human}\\ \boldsymbol{p}_{E}: & \text{proportion of exposed to approach human} \end{align}\]

\[\begin{aligned} A. \quad & \mathrm{H}_0: p_{\mathrm{E}}=p_{\mathrm{C}}, \mathrm{H}_{\mathrm{a}}: p_{\mathrm{E}}<p_{\mathrm{C}} \\ B. \quad & \mathrm{H}_0: p_{\mathrm{E}}=p_{\mathrm{C}}, \mathrm{H}_{\mathrm{a}}: p_{\mathrm{E}}>p_{\mathrm{C}} \\ C. \quad & \mathrm{H}_0: p_{\mathrm{E}}<p_{\mathrm{C}}, \mathrm{H}_{\mathrm{a}}: p_{\mathrm{E}}=p_{\mathrm{C}} \\ D. \quad & \mathrm{H}_0: p_{\mathrm{E}}>p_{\mathrm{C}}, \mathrm{H}_{\mathrm{a}}: p_{\mathrm{E}}=p_{\mathrm{C}} \end{aligned}\]
Click for answer The correct answer is B. (since it now favors parasites if exposed mosquitoes approach humans more during this stage)

Before and after

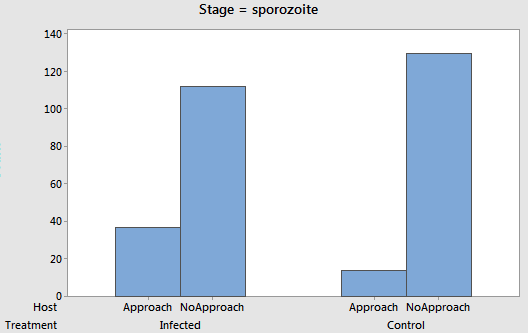
p̂E - p̂C =
20/113 - 36/117 =
0.177 - 0.308 = -0.131

p̂E - p̂C =
37/149 - 14/144 =
0.248 - 0.097 = 0.151

Is the difference significant?

The difference in proportions is 0.151 and the standard error is 0.05. Is this significant?

A. Yes

B. No

Malaria and Mosquitoes

It appears that mosquitoes infected by malaria parasites do, in fact, behave in ways advantageous to the parasites!

  • Exposed mosquitos are less likely to approach before becoming infectious (so more likely to stay alive)
  • Exposed mosquitos are more likely to approach humans after becoming infectious (so more likely to pass on disease)

Formula for p-values Using N(0,1)


\[\begin{align*} z=\frac{\text { sample statistic }-\text { null value }}{\text { SE }} \end{align*}\]

From original
data

From Ho

From
randomization
distribution

Connecting Normal model to Confidence Intervals

Suppose: bootstrap distribution is bell-shaped.

  • Center: sample statistic
  • Spread: the standard error given in the bootstrap graph (or by formula)

Bootstrap Distributions

If a bootstrap distribution is normally distributed, we can write it as

A. \(\mathrm{N} (parameter, SD)\)

B. \(\mathrm{N} (statistic, SD)\)

C. \(\mathrm{N} (parameter, SE)\)

D. \(\mathrm{N} (statistic, SE)\)

Click for answer The correct answer is D. (center = statistic, spread = SE)

Connecting Normal model to Confidence Intervals

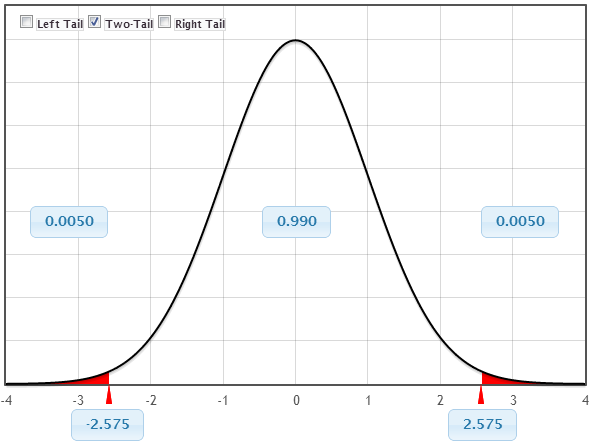
To get a \(95 \%\) confidence interval we compute: \[statistic \pm 2(SE)\]

Why 2 SE’s?

  • \(95 \%\) of all sample means fall within 2 SE’s of the population mean
  • The value 2 is a z-score!
  • Well, actually the precise z-score under a normal model is \(z=1.96\) instead of 2 !

N(0,1) model

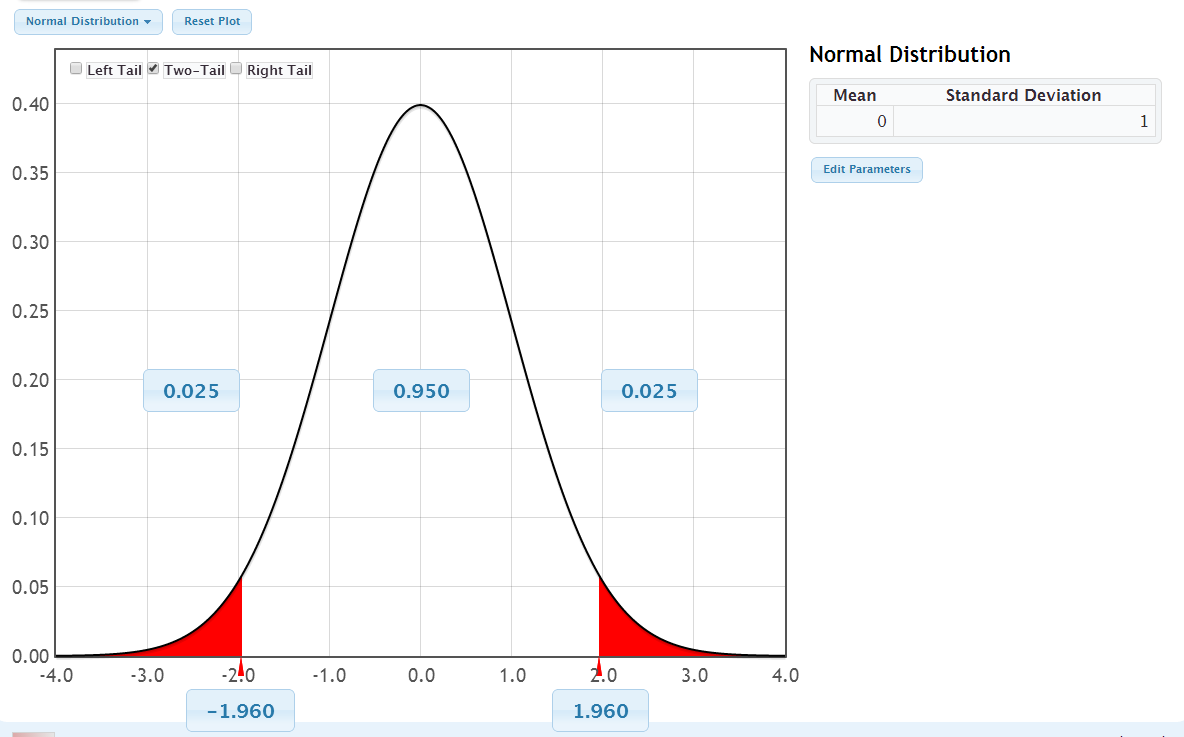
95% of all values fall within 1.96 SE’s of the mean

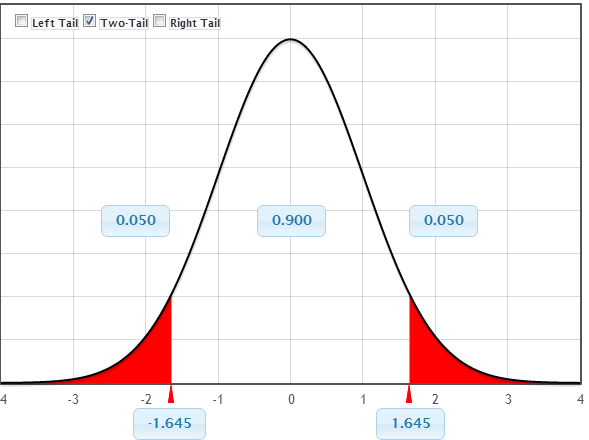
What if we wanted a 90% CI? What z-score should we use?

qnorm(0.95)
[1] 1.644854

90% Confidence: \(z^*=1.645\)

qnorm(0.995)
[1] 2.575829

99% Confidence: \(z^*=2.576\)

Confidence Interval using N(0,1)

If a statistic is normally distributed, we find a confidence interval for the parameter using \[statistic \pm z^* SE\] where the area between \(-z^*\) and \(+z^*\) in the standard normal distribution is the desired level of confidence.

 Group Activity 1


30:00