Inference for one mean

STAT 120

Bastola

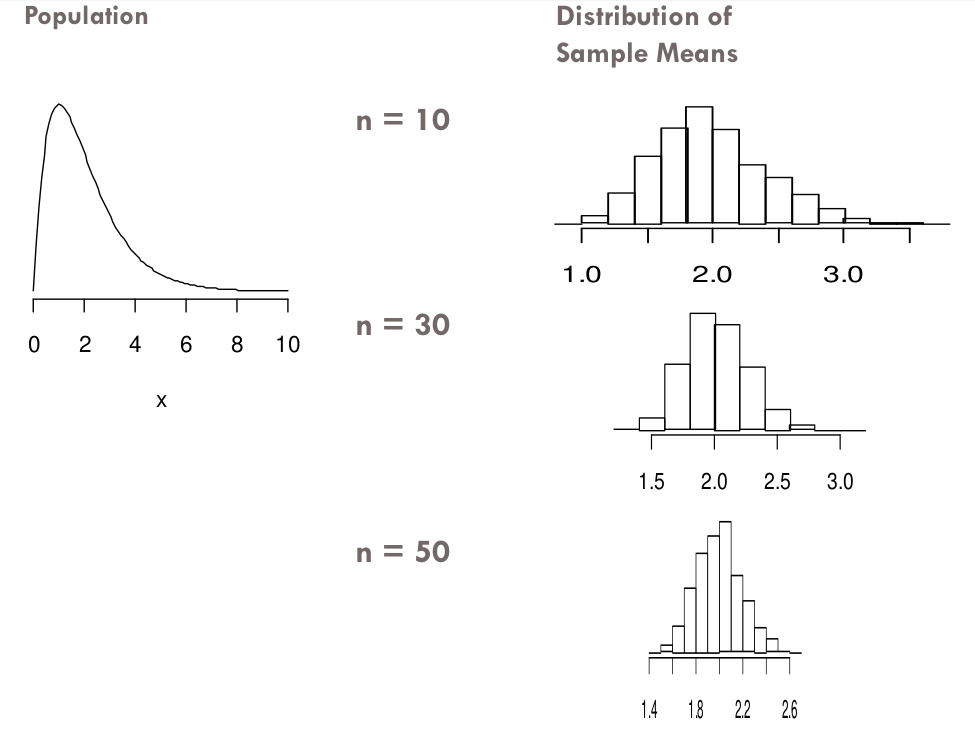
CLT for a Mean

If \(n \geq 30^*\), then

\[\bar{X} \approx N\left(\mu, \frac{\sigma}{\sqrt{n}}\right)\]

*Smaller sample sizes may be sufficient for symmetric distributions, and 30 may not be sufficient for very skewed distributions or distributions with high outliers

CLT for mean

Standard Deviation

The standard deviation of the population is

  1. \(\sigma\)

  2. \(s\)

  3. \(\frac{\sigma}{\sqrt{n}}\)


Click for answer The correct answer is a.

Standard Deviation

The standard deviation of the sample is

  1. \(\sigma\)
  2. \(s\)
  3. \(\frac{\sigma}{\sqrt{n}}\)

Click for answer The correct answer is b.

Standard Deviation

The standard deviation of the sample mean is

  1. \(\sigma\)
  2. \(s\)
  3. \(\frac{\sigma}{\sqrt{n}}\)

Click for answer The correct answer is c. The standard error is the standard deviation of the statistic.

T-distribution

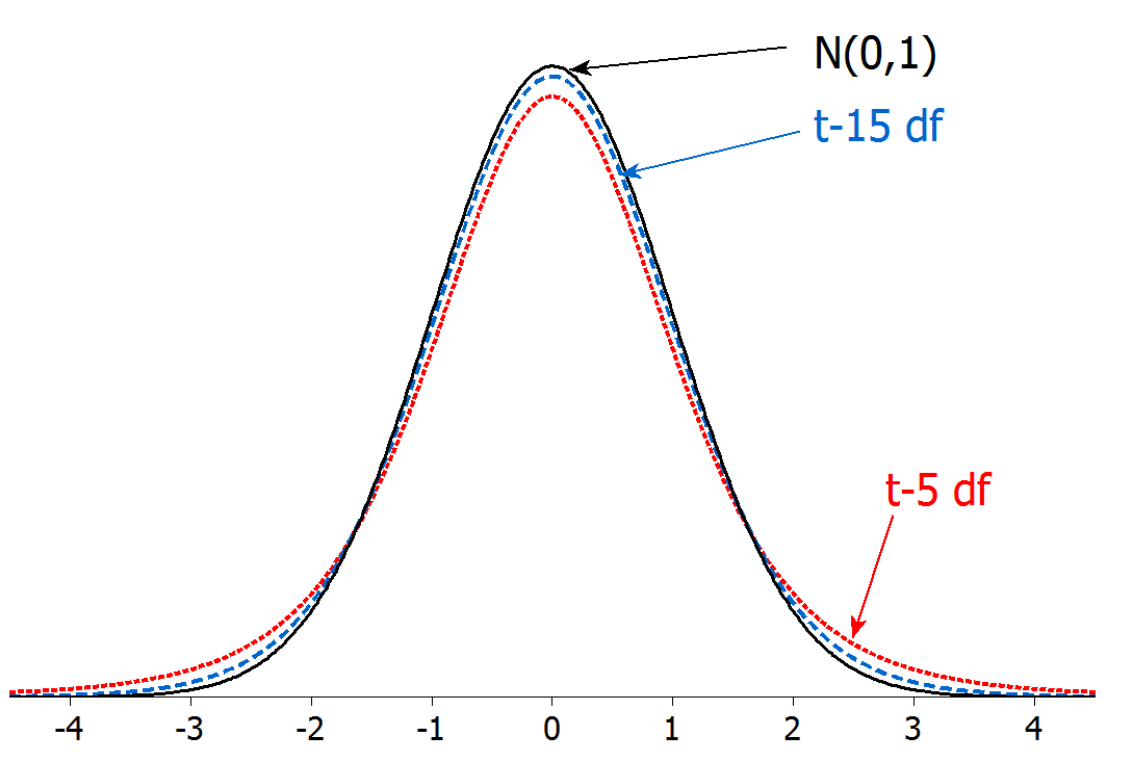
  • Replacing \(\sigma\) with \(s\) changes the distribution of the z-statistic from a normal distribution to a t-distribution
  • The \(t\) distribution is very similar to the standard normal, but with slightly fatter tails to reflect this added uncertainty

T-distribution


Inference for means: Hypothesis tests

Check: Check the one sample size conditions for the CLT

Tests: Use t-ratios of the form \[t=\frac{\text { stat }-\text { null value }}{S E}\] P-values computed from a t-distribution with appropriate \(\mathrm{df}\) - pt(t, df= ) gives the area to the left of \(t\)

Confidence intervals: \(\mathrm{CI}\) of the form \[\text { stat } \pm t^{*} S E\] The \(t^{*}\) multiplier comes from a t-distribution with appropriate \(d f\) - qt(0.975, df= ) gives \(t^{*}\) for \(95 \%\) confidence

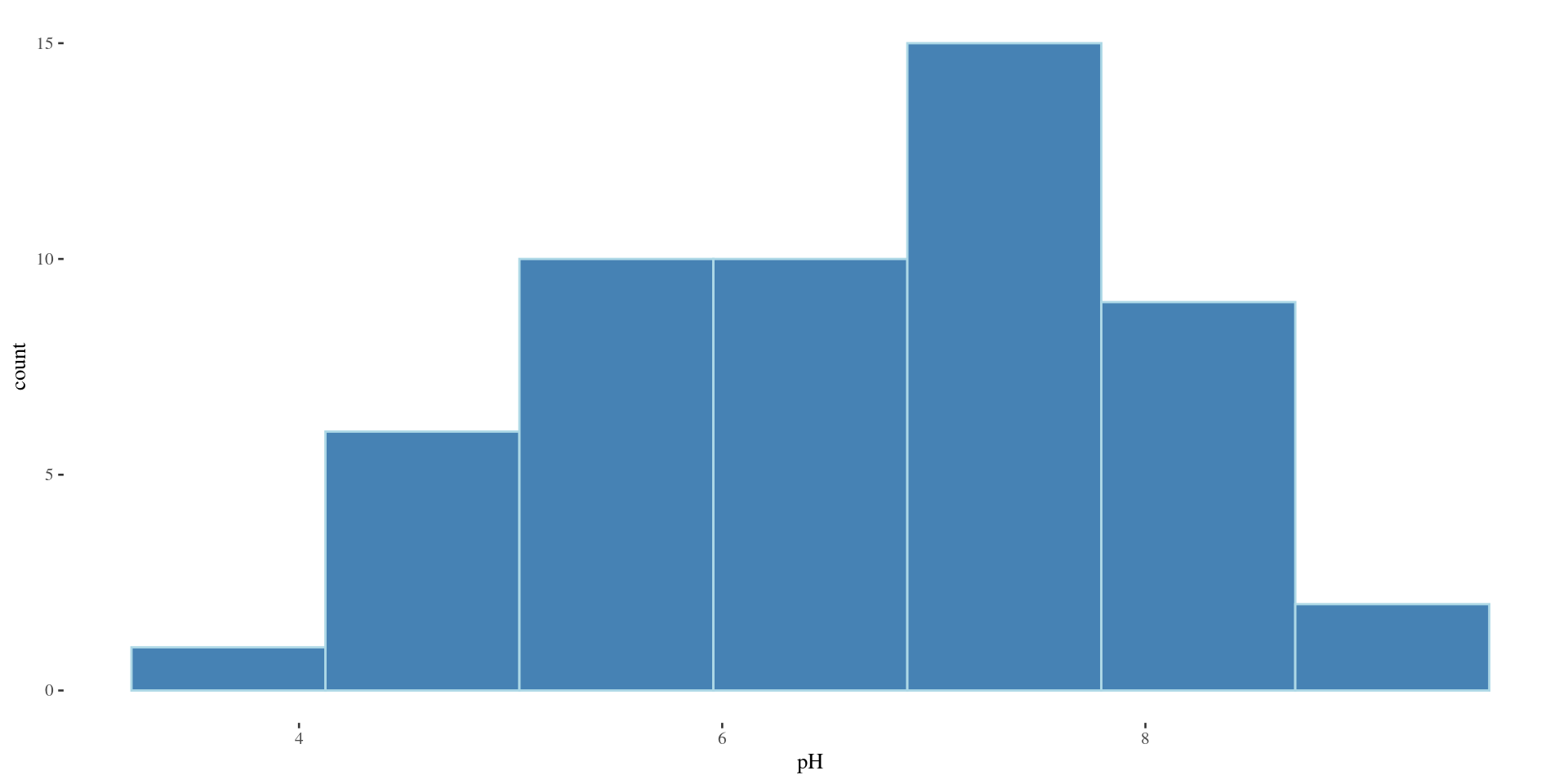
Florida lakes

53 lakes were sampled, pH recorded

  • Is average pH in Florida lakes different from 7 (neutral)?
  • Let \(\mu\) be the mean pH for all Florida lakes \[H_0: \mu = 7 \qquad\qquad H_A: \mu \neq 7\]

Can we use a t-test?

  • \(n=53\) is a decent sample size
  • check sample distribution of pHs

Florida lakes

library(ggplot2)
lakes <- read.csv("http://www.lock5stat.com/datasets2e/FloridaLakes.csv")
ggplot(lakes, aes(x = pH)) +
  geom_histogram(fill = "steelblue", 
                 bins = 7,
                 col = "lightblue")

Florida lakes

\[H_0: \mu = 7 \qquad H_A: \mu \neq 7\] Data: The average pH was \(\bar{x}=6.591\) with a standard deviation of \(s=1.288\).

mean(lakes$pH)
## [1] 6.590566
sd(lakes$pH)
## [1] 1.288449
  • The t-test stat is \(t = \dfrac{6.591 - 7}{1.288/\sqrt{53}} \approx -2.31\)
  • Interpret t: The observed mean of 6.591 is 2.31 SEs below 7.

Florida lakes

\[H_0: \mu = 7 \qquad\qquad H_A: \mu \neq 7\] - p-value \(2 \times P(t < -2.31)\), or double left tail area below -2.31 - use t-distribution with \(df = 53-1= 52\)

2*pt(-2.31, df=53-1)  # df = n-1
## [1] 0.02489032

  • Interpret: The p-value is 0.025. If the mean pH of all lakes is 7, then we would see a sample mean that is at least 2.31 SEs away from 7 about 2.5% of the time in samples of 53 lakes.

  • Conclusion: There is a statistically discernible difference between the observed mean pH of 6.591 and the hypothesized mean of 7 (t=-2.31, df=52, p=0.025).

Florida lakes: t.test in R

We can also use t.test in R !

t.test(lakes$pH, mu  = 7)

    One Sample t-test

data:  lakes$pH
t = -2.3134, df = 52, p-value = 0.02469
alternative hypothesis: true mean is not equal to 7
95 percent confidence interval:
 6.235425 6.945707
sample estimates:
mean of x 
 6.590566

Florida lakes

How different is the population mean from 7?

  • 95% CI for \(\mu\):

\[6.591 \pm 2.0066 \dfrac{1.288}{\sqrt{53}} = 6.591 \pm 0.355 = (6.236, 6.946)\] where \(t^*\) corresponds to 95% confidence (97.5th percentile):

qt(.975, df=53-1)
## [1] 2.006647

We are 95% confident that the mean pH of all lakes is between 6.236 and 6.946 (slightly acidic)

Gribbles

Gribbles are small marine worms that bore through wood, and the enzyme they secrete may allow us to turn inedible wood and plant waste into biofuel

  • A sample of 50 gribbles finds an average length of \(3.1 \mathrm{~mm}\) with a standard deviation of \(0.72 \mathrm{~mm}\).

  • Give a \(90 \%\) confidence interval for the average length of gribbles.


Gribbles

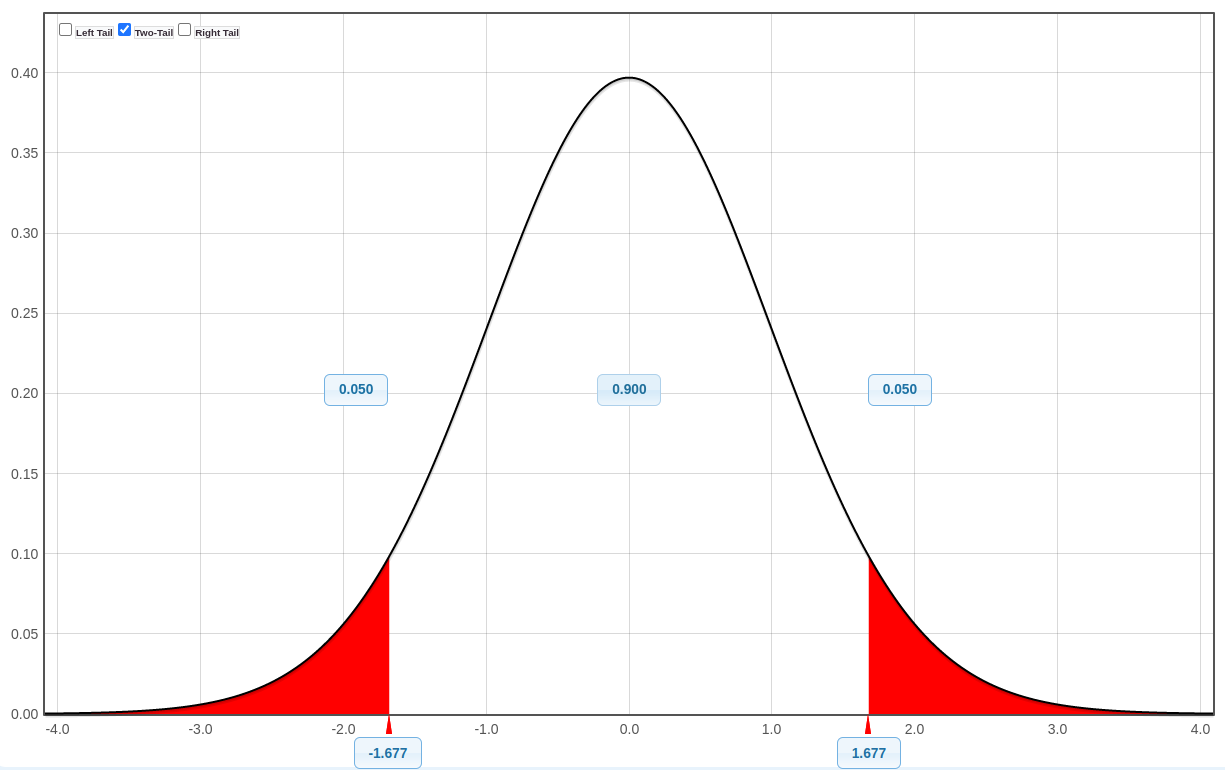
A sample of 50 gribbles finds an average length of \(3.1 \mathrm{~mm}\) with a standard deviation of \(0.72 \mathrm{~mm}\). For a \(90 \%\) confidence interval for the average length of gribbles, what is \(t^*\) ?

a). 1.645 b). 1.677 c). 1.960 d). 1.690


Click for answer \(d f=n-1=49 \text { and } t^*=1.677\)

Gribbles

A sample of 50 gribbles finds an average length of \(3.1 \mathrm{~mm}\) with a standard deviation of \(0.72 \mathrm{~mm}\). For a \(90 \%\) confidence interval for the average length of gribbles, what is the standard error?

a). 0.171 b). 0.720 c). 1.960 d). 0.102


Click for answer \(\frac{s}{\sqrt{n}}=\frac{0.72}{\sqrt{50}}=0.102\)

Gribbles

A sample of 50 gribbles finds an average length of \(3.1 \mathrm{~mm}\) with a standard deviation of \(0.72 \mathrm{~mm}\). For a \(90 \%\) confidence interval for the average length of gribbles, what is the margin of error?

a). 0.171 b). 0.720 c). 1.960 d). 0.102


Click for answer \(t^* \cdot \frac{s}{\sqrt{n}}=1.677 \cdot \frac{0.72}{\sqrt{50}}=0.171\)

Gribbles

\(\begin{gathered}\text { statistic } \pm t^* \cdot S E \\ \bar{x} \pm t^* \cdot \frac{s}{\sqrt{n}} \\ 3.1 \pm 1.677 \cdot \frac{0.72}{\sqrt{50}} \\ 3.1 \pm 0.17 \\ (2.93,3.27)\end{gathered}\)


We are \(90 \%\) confident that the average length of gribbles is between 2.93 and \(3.27 \mathrm{~mm}\).

Margin of error

\[\mathrm{CI}: \bar{x} \pm t^* \cdot \frac{s}{\sqrt{n}}\]

For a single mean, what is the margin of error?

  1. \(\frac{s}{\sqrt{n}}\)
  2. \(t^* \cdot \frac{s}{\sqrt{n}}\)
  3. \(2 \cdot \mathrm{t}^* \cdot \frac{s}{\sqrt{n}}\)

Click for answer \(\text {CI = statistic } \pm \text { margin of error }\)