Inference for multiple proportions: One Categorical Variable

STAT 120

Bastola

Tests for One Categorical Variable

Goodness-of-fit test

  • Test a claim about the distribution of one categorical variable
  • E.g. are 6 M&M colors equally likely?
  • E.g. is Biden’s approval rating 50%?

Tests for One Categorical Variable

Seen single proportion tests before - Example : Test if the proportion of Reese’s Pieces that are orange is different from 1/3.

\[\begin{aligned} H_0 : p = 1/3\\ H_a : p \neq 1/3 \end{aligned}\]

What if we want to test proportions for several categories at once?

  • Example: Are the three colors (orange, yellow, brown) of Reese’s Pieces equally likely?

\(H_0\) specifies a proportion, \(p_i\) , for each category.

Rock-Paper-Scissors

ROCK PAPER SCISSORS TOTAL
36 12 37 85

How would we test whether all of these categories are equally likely?

Conduct a hypothesis test

  • State Hypothesis
  • Calculate a test statistic, based on your sample data
  • Create a distribution of this statistic, as it would be observed if the null hypothesis were true
  • Measure how extreme your test statistic is, as compared to the distribution generated under null

Test Statistic

Why can’t we use the familiar formula to get the test statistic?

\[\frac{\text { sample statistic - null value }}{\text { SE }}\]

  • More than one sample statistic
  • More than one null value

We need something a bit more complicated …

Observed Counts

The observed counts are the actual counts observed in the study

ROCK PAPER SCISSORS TOTAL
36 12 37 85
  • The expected counts are the expected counts if the null hypothesis were true
  • For each cell, the expected count is the sample size \(n\) times the null proportion, \(p_o\)
  ROCK PAPER SCISSORS TOTAL
Observed 36 12 37 85
Expected 28.33 28.33 28.33 85

Chi-Square Statistic

  • A test statistic is one number, computed from the data, which we can use to assess the null hypothesis
  • The chi-square statistic is a test statistic for categorical variables:
\[\begin{aligned} \chi^2 = \sum{\frac{(observed - expected)^2}{expected}} = \sum{\frac{(O - E)^2}{E}} \end{aligned}\]

Rock-Paper-Scissors

  ROCK PAPER SCISSORS TOTAL
Observed 36 12 37 85
Expected 28.33 28.33 28.33 85
\[\begin{aligned} \chi^2 &= \frac{(36-28.33)^2}{28.33} + \frac{(12 - 28.33)^2}{28.33} + \frac{(37 - 28.33)^2}{28.33}\\ &= 2.076 + 9.379 + 2.628 \\ &= 14.083 \end{aligned}\]

What next?

We have a test statistic. What else do we need to perform the hypothesis test? - A distribution of the test statistic assuming \(H_0\) is true

How do we get this? Two options:

  1. Simulation
  2. Theoretical Distribution

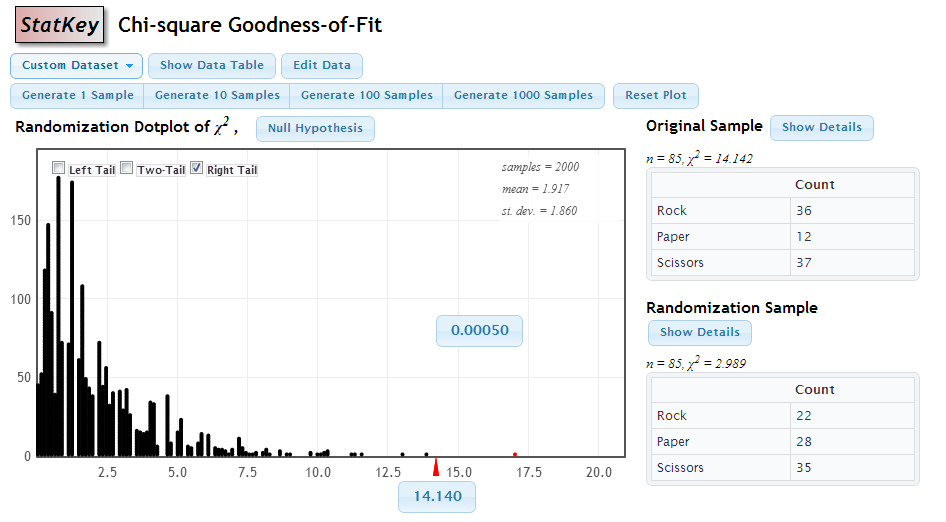
Simulation

  1. Take 3 scraps of paper and label them Rock, Paper, Scissors. Fold or crumple them so they are indistinguishable. Choose one at random and record the result.

  2. Repeat a number of times to match the original sample size and get a table of observed counts.

  3. Calculate the \(\chi^{2}\)-statistic.

  4. Repeat this many times to get a randomization distribution of many \(\chi^{2}\)-statistics.

  5. How extreme is the actual test statistic in this randomization distribution?

Statkey: Chi-Square Distribution


Chi-Square Distribution

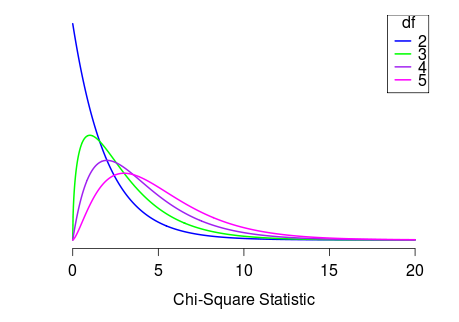
If each of the expected counts are at least 5, AND if the null hypothesis is true, then the \(\chi^2\) statistic follows a \(\chi^2\) distribution, with degrees of freedom equal to

\[df = \text{number of categories} -1\]

Rock-Paper-Scissors:

df = 3 - 1 = 2 # degrees of freedom

Chi-Square Distribution


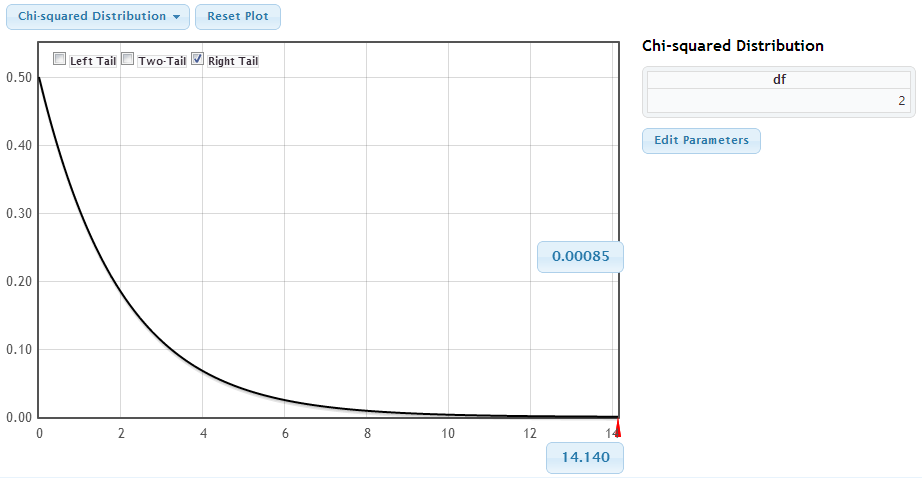
Statkey: p-value using Chi-square distribution


Goodness of Fit

  • A \(\chi^2\) test for goodness of fit test determines whether the distribution of a categorical variable is the same as some null hypothesized distribution

  • The null hypothesized proportions for each category do not have to be the same

Chi-Square Test for Goodness of Fit

  • State null hypothesized proportions for each category, pi. Alternative is that at least one of the proportions is different than specified in the null.

  • Calculate the expected counts for each cell as \(n\cdot p_i\). Make sure they are all greater than 5 to proceed.

  • Calculate the \(\chi^2\) statistic: \(\chi^2 = \sum{\frac{(observed - expected)^2}{expected}}\)

  • Compute the p-value as the area in the tail above the \(\chi^2\) statistic, for a \(\chi^2\) distribution with \(df = (\text{number of categories - 1})\).

  • Interpret the p-value in context and conclude.

 Group Activity 1


30:00