Stat120 Spring24 – Inference for multiple proportions: Two Categorical Variables

Tests for Categorical Variable(s)

Chi-square test for association

Determine if a relationship between two categorical variables is statistically significant
E.g. Does M&M color distribution depend on type (chocolate vs. peanut)?

Chi-square test for association hypothesis

Hypotheses look like:

E.g. Does M&M color distribution depend on type (chocolate vs. peanut)?

Expected Counts and p-value

The expected counts for each combination in a two-way table

Large chi-square test stat values support the alternative hypothesis so:
always a right-tailed value

Chi-Square test for association: P-VALUE

randomization/permutation: simulate new data consistent with and recompute the test stat

Association: permute the values of one variable column to break the link that could exist in the data between both variables

Chi-square distribution (probability model):

Association: use where number of rows and number of columns
need large enough so expected counts are at least 5

Example: Does political comfort level depend on religion?

There is no association between religion and comfort level

implies: the distribution of comfort level is the same for all three religion types

There is an association between religion and comfort level

implies: the distribution of comfort level is the different for at least one religion type.

Association example

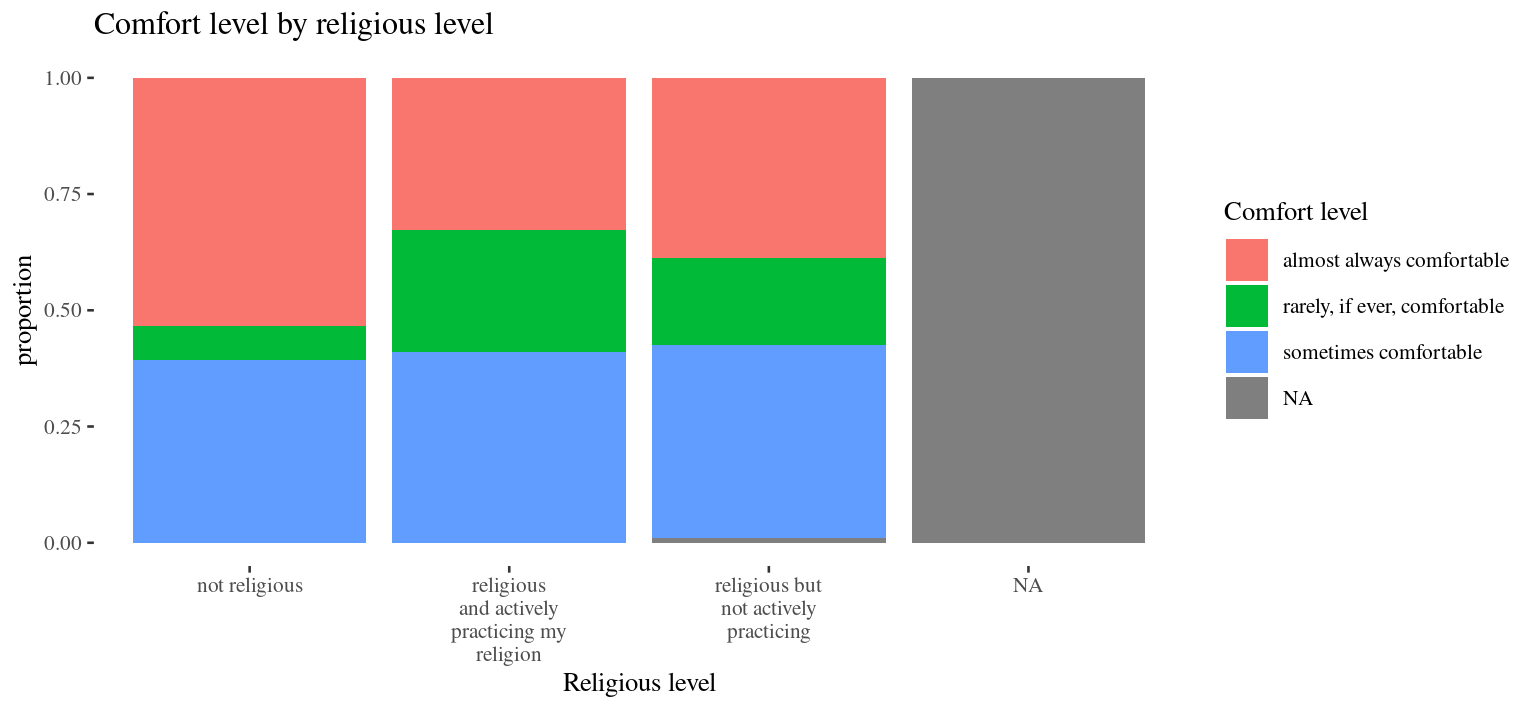
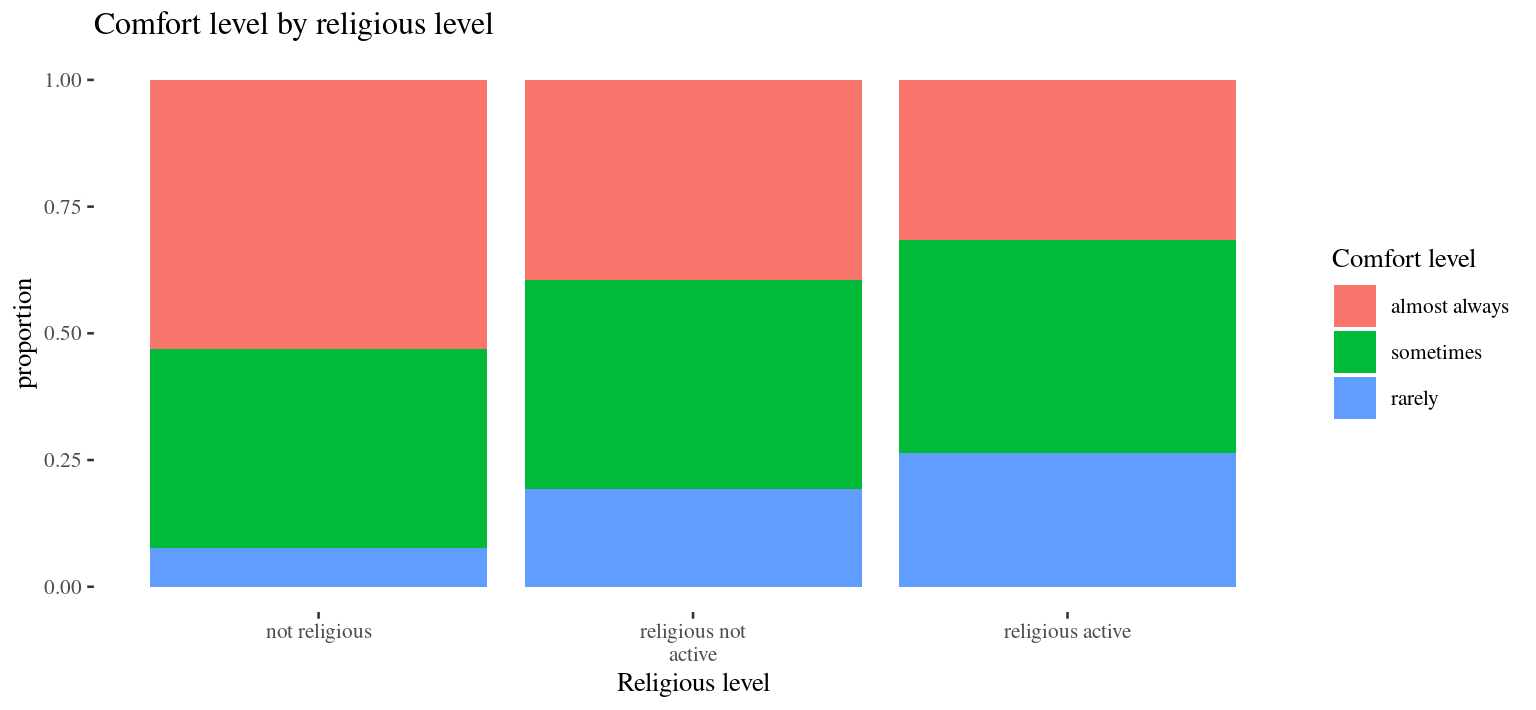
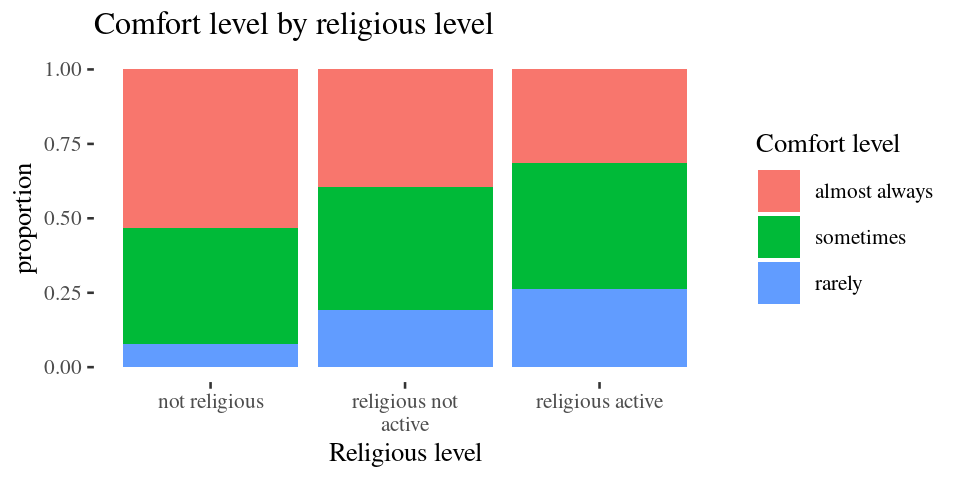
survey <- read.csv("https://raw.githubusercontent.com/deepbas/statdatasets/main/Survey.csv")
survey %>% dplyr::select(Question.8, Question.9) %>% head()

                             Question.8                Question.9
1                         not religious almost always comfortable
2                         not religious     sometimes comfortable
3                         not religious almost always comfortable
4 religious but not actively practicing almost always comfortable
5                         not religious     sometimes comfortable
6                         not religious almost always comfortable

Table 1: A two way table of religious preference and political comfortness
	almost always comfortable	rarely, if ever, comfortable	sometimes comfortable
not religious	110	15	81
religious and actively practicing my religion	20	16	25
religious but not actively practicing	41	20	44

Association example

Association Example

EDA for two categorical variables

drop missing values, rename column names
change/shorten comfort level names
reorder the levels

Observed distribution of political comfort level given religiousness

Table 2: A two way table of religious preference and political comfortness (cleaned-up factors)
	almost always	sometimes	rarely
not religious	103	76	15
religious not active	39	41	19
religious active	18	24	15

Association example

counts <- table(survey$religiousness, survey$comfortness)
counts
##                       
##                        almost always sometimes rarely
##   not religious                  103        76     15
##   religious not active            39        41     19
##   religious active                18        24     15

prop.table(counts,1)  
##                       
##                        almost always  sometimes     rarely
##   not religious           0.53092784 0.39175258 0.07731959
##   religious not active    0.39393939 0.41414141 0.19191919
##   religious active        0.31578947 0.42105263 0.26315789

There is a much higher rate of “almost always” comfortable for the not religious respondents (53.1%) than those that are religious (not active: 39.4%; active: 31.6%).

Association example

Expected counts assuming no association (null)?

expected number of respondents who are “not religious” and “almost always comfortable”?
is not 1/9 of all respondents!

Association example

There are 194 “not religious” respondents (row total)
The overall rate (ignoring religion) of “almost always comfortable” is , or about 45.7%.
If religion isn’t related to comfort level, the expected number is about

Association example

Chi-square contribution for “not religious” and “almost always comfortable” cell?

The contribution to the chi-square test stat from this category is 2.31.

Association example: `chisq.test`

ComfortReligion <- chisq.test(survey$religiousness, survey$comfortness)
ComfortReligion


    Pearson's Chi-squared test

data:  survey$religiousness and survey$comfortness
X-squared = 19.33, df = 4, p-value = 0.0006768

The test stat value is 19.33.
There are 3 categories for each variable, so the degrees of freedom will be .

Association example

Interpret: If there is no association between comfort level and religiousness, then we would see a chi-square test stat of 19.33, or one even larger, only about 0.07% of the time.
Conclusion: We have strong evidence that there is an association between political comfort level and religiousness ( , df = 4, p-value = 0.0007).

Association example: Check Assumptions!

Are the expected counts above 5?

ComfortReligion <- chisq.test(survey$religiousness, survey$comfortness)
ComfortReligion$expected

                      survey$comfortness
survey$religiousness   almost always sometimes rarely
  not religious             88.68571  78.15429  27.16
  religious not active      45.25714  39.88286  13.86
  religious active          26.05714  22.96286   7.98

Association example

If we get a red warning when running chisq.test, it usually means the sample size conditions aren’t met to use the chi-square model.
Instead run a randomization test with simulate.p.value = TRUE

chisq.test(survey$religiousness, survey$comfortness, 
           simulate.p.value = TRUE)


    Pearson's Chi-squared test with simulated p-value (based on 2000
    replicates)

data:  survey$religiousness and survey$comfortness
X-squared = 19.33, df = NA, p-value = 0.0009995

Association example

Describe the association!

which groups have the most different comfort levels?

Association example

95% CI for the difference in the true proportions of “rarely comfortable” people in the not religious and actively religious groups.

95% CI for

table(survey$religiousness)


       not religious religious not active     religious active 
                 194                   99                   57

Association example

knitr::kable(counts)

	almost always	sometimes	rarely
not religious	103	76	15
religious not active	39	41	19
religious active	18	24	15

knitr::kable(round(prop.table(counts,1),3))

	almost always	sometimes	rarely
not religious	0.531	0.392	0.077
religious not active	0.394	0.414	0.192
religious active	0.316	0.421	0.263

Association example

95% CI for

I am 95% confident that the percentage of all non-religious students who are rarely comfortable is between 6.6 to 30.6 percentage points lower than the actively religious students.

Please download the Class-Activity-23 template from moodle and go to class helper web page

30:00