Comparing Two or more Means

STAT 120

Bastola

Inference tools (Classical methods)

Categorical Response

One proportion: sample z test/CI
Difference in 2 props: 2 sample z test/CI OR chi-square test
Association between 2 categorical variables: chi-square test

Quantitative Response

One mean: 1 sample t test/CI
Difference in 2 means: 2 independent sample t test/CI OR Matched pairs
Compare >2 means: One-way ANOVA

Multiple Categories

So far, we’ve learned how to do inference for a difference in means IF the categorical variable has only two categories (i.e. compare two groups)

In this section, we’ll learn how to do hypothesis tests for a difference in means across multiple categories (i.e. compare more than two groups)

Hypotheses

To test for a difference in true/population means across k groups:

\[\begin{align*} H_{0}:& \quad \mu_{1}=\mu_{2}=\ldots=\mu_{k}\\ H_{a}:& \quad \text{At least one } \mu_{i} \neq \mu_{j} \end{align*}\]

Frisbee Example

Does Frisbee grip affect the distance of a throw?

A student performed the following experiment: 3 grips, 8 throws using each grip

1. Normal grip
2. One finger out grip
3. Frisbee inverted grip

A grip type is randomly assigned to each of the 24 throws she plans on making

Response: measured in paces how far her throw went
Question: How might you summarize her data?

Frisbee Example

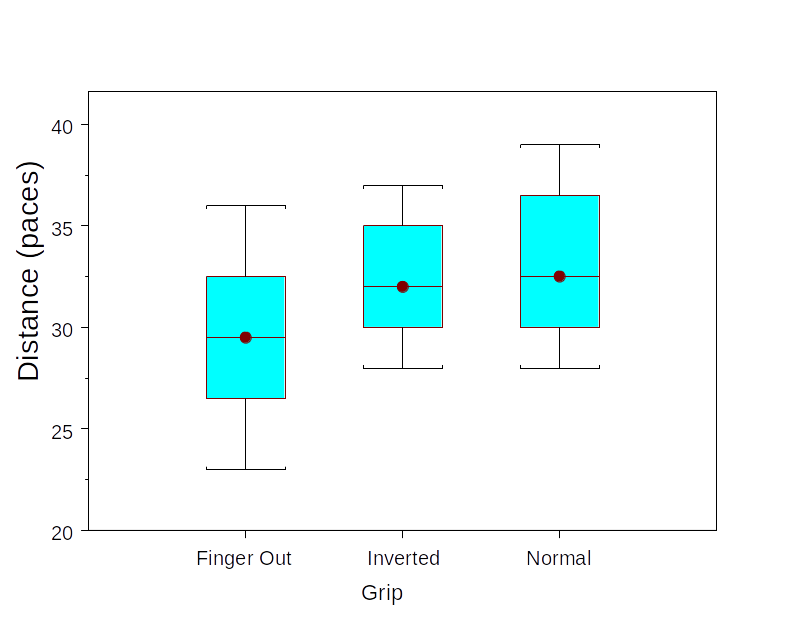
	Finger-out	Inverted	Normal
n	8	8	8
Mean	29.5	32.375	33.125
SD	4.175	3.159	3.944

Question: Is this evidence that grip affects mean distance thrown? \[\begin{align*} H_{0}:& \quad \mu_{1}=\mu_{2}=\mu_{3}\\ H_{a}:& \quad \text{At least one } \mu_{1}, \mu_{2}, \mu_{3} \text{ is not the same} \end{align*}\]

:::

Why Analyze Variability to Test for a Difference in Means?

The group means in Datasets \(A\) and \(B\) are the same, but the boxes show different spread.
Datasets \(A\) and \(C\) have the same spread for the boxes, but different group means.

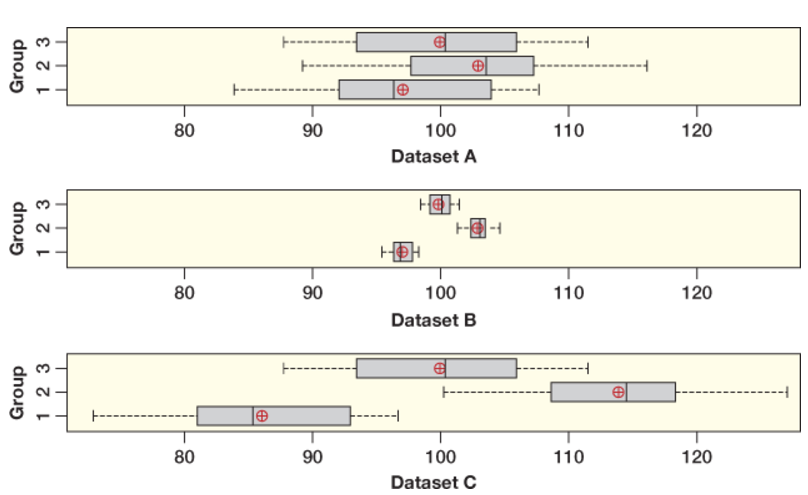
Which of these graphs appear to give strong visual evidence for a difference in the group means?

Why Analyze Variability to Test for a Difference in Means?

Dataset A = weakest evidence for a difference in means.

Datasets B and C = strong evidence for a difference in means.

Why Analyze Variability to Test for a Difference in Means?

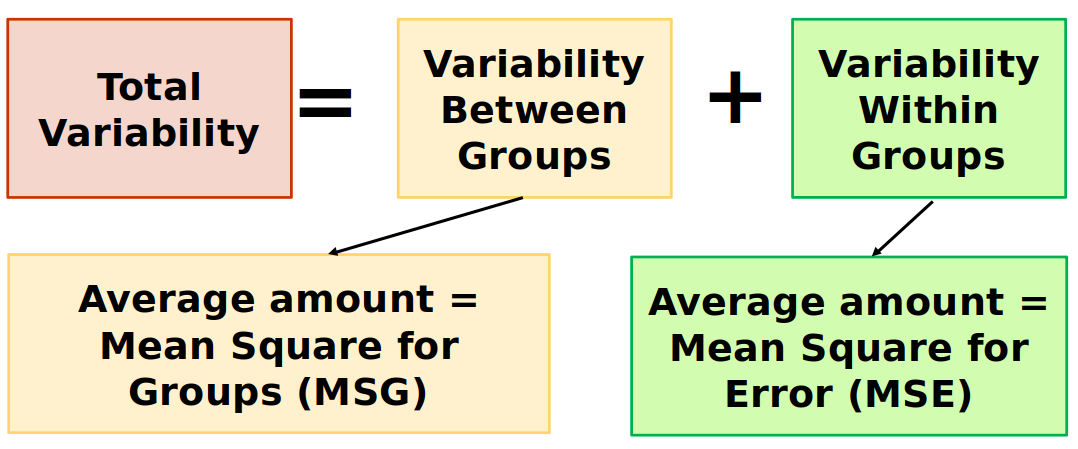
Conclusion: An assessment of the difference in means between several groups depends on two kinds of variability:

How different the means are between each groups
The amount of variability within each groups

Analysis of Variance

Analysis of Variance (ANOVA) compares the variability between groups to the variability within groups

F-Statistic

The F-statistic is a ratio: \[F=\frac{M S G}{M S E}=\frac{\text { average between group variability }}{\text { average within group variability }}\]

If there really is a difference between the groups \((H_A \text{ true})\), we would expect the F-statistic to be

a). Large positive

b). Large negative

c). Close to 0

Click for answer

The correct answer is a.

Frisbee Example

frisbee <- read.csv("https://raw.githubusercontent.com/deepbas/statdatasets/main/Frisbee.csv")
frisbee.anova <- aov(Distance ~ Grip, data = frisbee) # fit an ANOVA model

summary(frisbee.anova)

            Df Sum Sq Mean Sq F value Pr(>F)
Grip         2  58.58   29.29   2.045  0.154
Residuals   21 300.75   14.32

F-test statistic: 2.045

P-value: 0.154

How to determine significance?

We have a test statistic. What else do we need to perform the hypothesis test?

A distribution of the test statistic assuming \(H_0\) is true.

How do we get this? Two options:

Simulation
Theory

`CarletonStats` R package

library(CarletonStats)
permTestAnova(Distance ~ Grip, data = frisbee)


    ** Permutation test **

 Permutation test with alternative: greater 
 Observed F statistic: 2.0453 
 Mean of permutation distribution: 1.10846 
 Standard error of permutation distribution: 1.2343 
 P-value:  0.156 

    *-------------*

F-Distribution

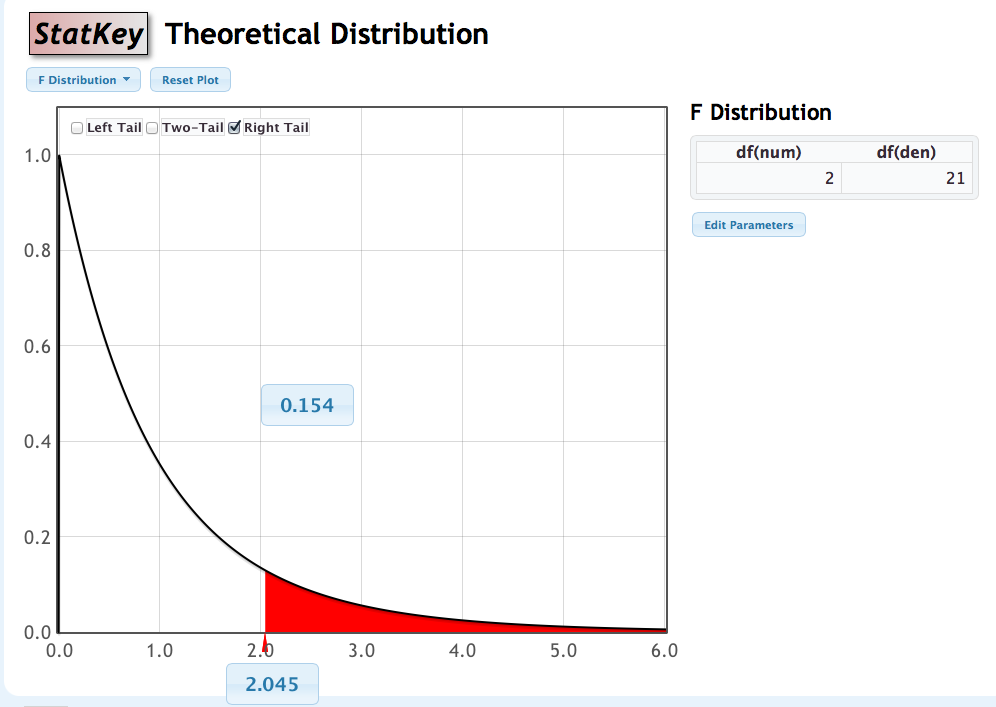
We can use the F-distribution to generate a p-value if:

Sample sizes in each group are large (each \(n_{i} \geq 30\) ) OR the data within each group are relatively normally distributed
Variability is similar in all groups

The F-distribution has two degrees of freedom, one for the numerator of the ratio \((\boldsymbol{k}-\mathbf{1})\) and one for the denominator \((n-k)\)
For F-statistics, the p-value (the area as extreme or more extreme) is always the right tail

F-distribution

An F-statistic as large as 2.045 would occur by chance about 16% of the time if the means were all equal.
Our results are inconclusive and do not support the claim that grips affects average distance.

1 - pf(2.045,2,21)  # p-value

[1] 0.1543639

Check assumptions: normality

table(frisbee$Grip)  # check n's


Finger Out   Inverted     Normal 
         8          8          8

Small \(n_i\) but all groups are roughly normal

# checking normality with qq-plots
ggplot(frisbee, aes(sample = Distance)) + 
  geom_qq() + geom_qq_line() +  facet_wrap(~Grip) +  
  theme(axis.text.x = element_text(size = 4))

Check Assumptions: Equal Variance

The F-distribution assumes equal within group variability for each group. This is also an assumption when using the randomization distribution.

As a rough rule of thumb, this assumption is violated if the largest group standard deviation is more than double the smallest group standard deviation

tapply(frisbee$Distance, frisbee$Grip, sd)

Finger Out   Inverted     Normal 
  4.174754   3.159453   3.943802

Ensure:

\(\frac{\text{largest }s}{\text{smallest }s} < 2\)

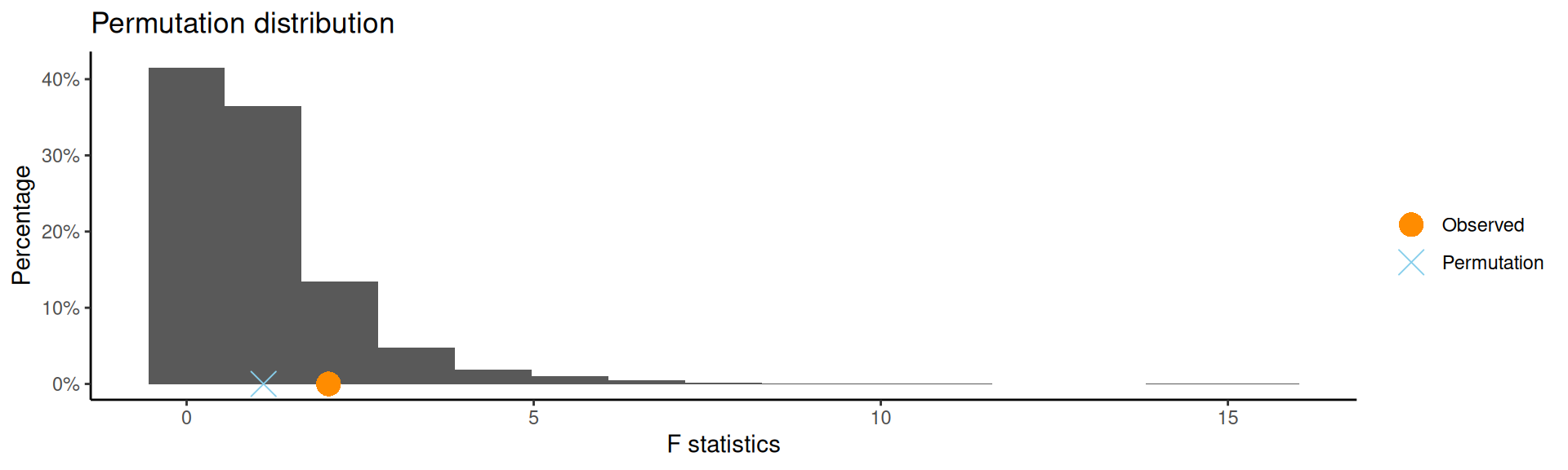
Frisbee Example: Inference

Question: Is this evidence that grip affects mean distance thrown?

\[\begin{align*} H_{0}:& \quad \mu_{1}=\mu_{2}=\mu_{3}\\ H_{a}:& \quad \text{At least one } \mu_{1}, \mu_{2}, \mu_{3} \text{ is not the same} \end{align*}\] \(\mu_{\mathrm{i}}\) is the true mean distance thrown using grip \(i\). \[F=2.05(\mathrm{df}=2,21), \text {p-value}=0.1543\]

Conclusion: Do not reject the Null hypothesis. The difference in observed means is not statistically significant.

About 15% of the time we would see the grip differences like those observed, or even bigger, when there is actually no difference between the true mean distances thrown with different grips.

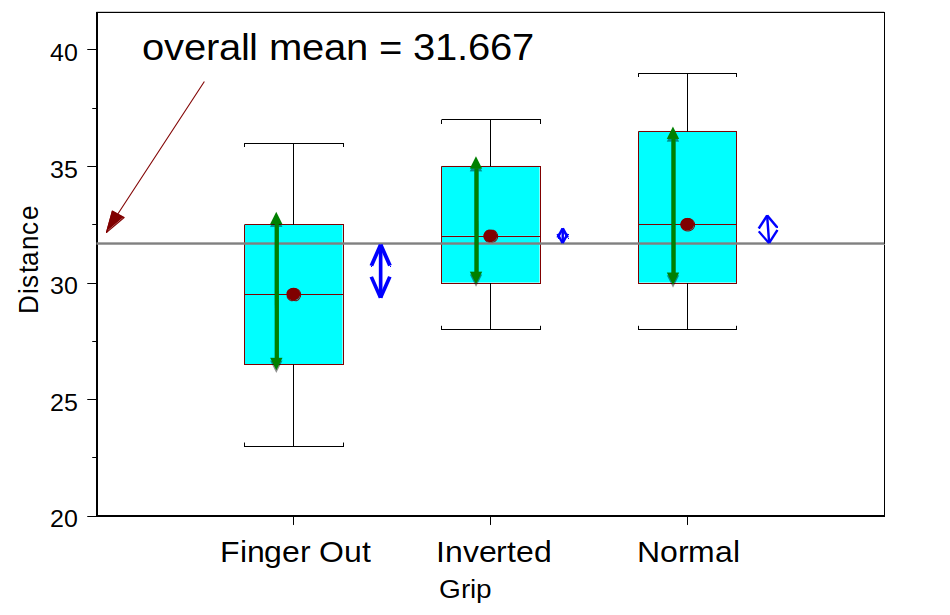
Picturing the variation

Green: Variation within groups

Blue: Variation between groups

ANOVA Table for Frisbee data

\[\text{F-test stat} = 29.29/14.32 = 2.045\]

Source	df	Sum of Squares	Mean Square
Groups	#groups -1 3-1 = 2	SSG 58.583	SSG/df 58.583/2 = 29.29
Error (residual)	n - #groups 24-3 = 21	SSE 300.750	SSE/df 300.75/21= 14.32
Total	n-1 24-1 = 23	SSTotal 359.333

ANOVA Table formula (don’t memorize!)

Source	df	Sum of Squares	Mean Square
Groups	\( k - 1 \)	\( \sum_{\text{groups}} n_i (\bar{x}_i - \bar{x})^2 \)	\( \frac{SSG}{k - 1} \)
Error (residual)	\( N - k \)	\( \sum_{\text{groups}} (n_i - 1) s_i^2 \)	\( \frac{SSE}{N - k} \)
Total	\( N - 1 \)	\( \sum_{\text{values}} (x_i - \bar{x})^2 \)

Frisbee Example: ANOVA table in R

frisbee.anova <- aov(Distance ~ Grip, data = frisbee)

summary(frisbee.anova)

            Df Sum Sq Mean Sq F value Pr(>F)
Grip         2  58.58   29.29   2.045  0.154
Residuals   21 300.75   14.32

library(broom) 
knitr::kable(tidy(frisbee.anova)) # nicer summary tables

term	df	sumsq	meansq	statistic	p.value
Grip	2	58.58333	29.29167	2.045303	0.1543247
Residuals	21	300.75000	14.32143	NA	NA

Please download the Class-Activity-24 template from moodle and go to class helper web page

30:00

Comparing Two or more Means

Inference tools (Classical methods)

Multiple Categories

Hypotheses

Frisbee Example

Frisbee Example

Why Analyze Variability to Test for a Difference in Means?

Why Analyze Variability to Test for a Difference in Means?

Why Analyze Variability to Test for a Difference in Means?

Analysis of Variance

F-Statistic

Frisbee Example

How to determine significance?

CarletonStats R package

F-Distribution

F-distribution

Check assumptions: normality

Check Assumptions: Equal Variance

Frisbee Example: Inference

Picturing the variation

ANOVA Table for Frisbee data

ANOVA Table formula (don’t memorize!)

Frisbee Example: ANOVA table in R

Group Activity 1

`CarletonStats` R package