Post-ANOVA

STAT 120

Bastola

Post-ANOVA

Inference AFTER doing ANOVA to compare means for several groups:

Confidence interval for a single mean
Confidence interval for a difference in two means
Pairwise t-test for a difference in two means
Multiple comparisons

ANOVA for Difference in Means

\[H_0:\mu_1 = \mu_2 = \cdots = \mu_k\] \[H_a: \text{at least one } \mu_i \text{ is different}\]

Conditions: Similar variability AND either sample sizes in each group are large (each \(n_i \geq 30\)) OR the data are relatively normally distributed

Cuckoo Birds

Cuckoo birds lay their eggs in the nests of other birds
When the cuckoo baby hatches, it kicks out all the original eggs/babies
If the cuckoo is lucky, the mother will raise the cuckoo as if it were her own

Cuckoo bird in nest

Do cuckoo bird eggs found in nests of different species differ in size?

Cuckoo Dataset

cuckoo dataset contains information on 120 Cuckoo eggs, obtained from randomly selected “foster” nests.
researchers have measured the length (in mm) and established the type (species) of foster parent.

Species=1: Hedge Sparrow
Species=2: Meadow Pit
Species=3: Pied Wagtail
Species=4: European Robin
Species=5: Tree Pipit
Species=6: Eurasian Wren

species	mean	sd	n
hedge.sparrow	23.11429	1.0494373	14
meadow.pipit	22.29333	0.9195849	45
pied.wagtail	22.88667	1.0722917	15
robin	22.55625	0.6821229	16
tree.pipit	23.08000	0.8800974	15
wren	21.12000	0.7542262	15

library(dplyr)
Cuckoo <- read.csv("https://raw.githubusercontent.com/deepbas/stat120datasets/main/cuckoos.csv")
Cuckoo <- Cuckoo %>%
  mutate(species = factor(species))   # change species to a categorical variable

stat <- Cuckoo %>% 
  group_by(species) %>%  # group by species
  summarize(mean = mean(length), # summary of quantitative var
            sd = sd(length), 
            n = length(length)) %>%
  data.frame()
knitr::kable(stat)

Side-by-side Boxplot

Plot
Code

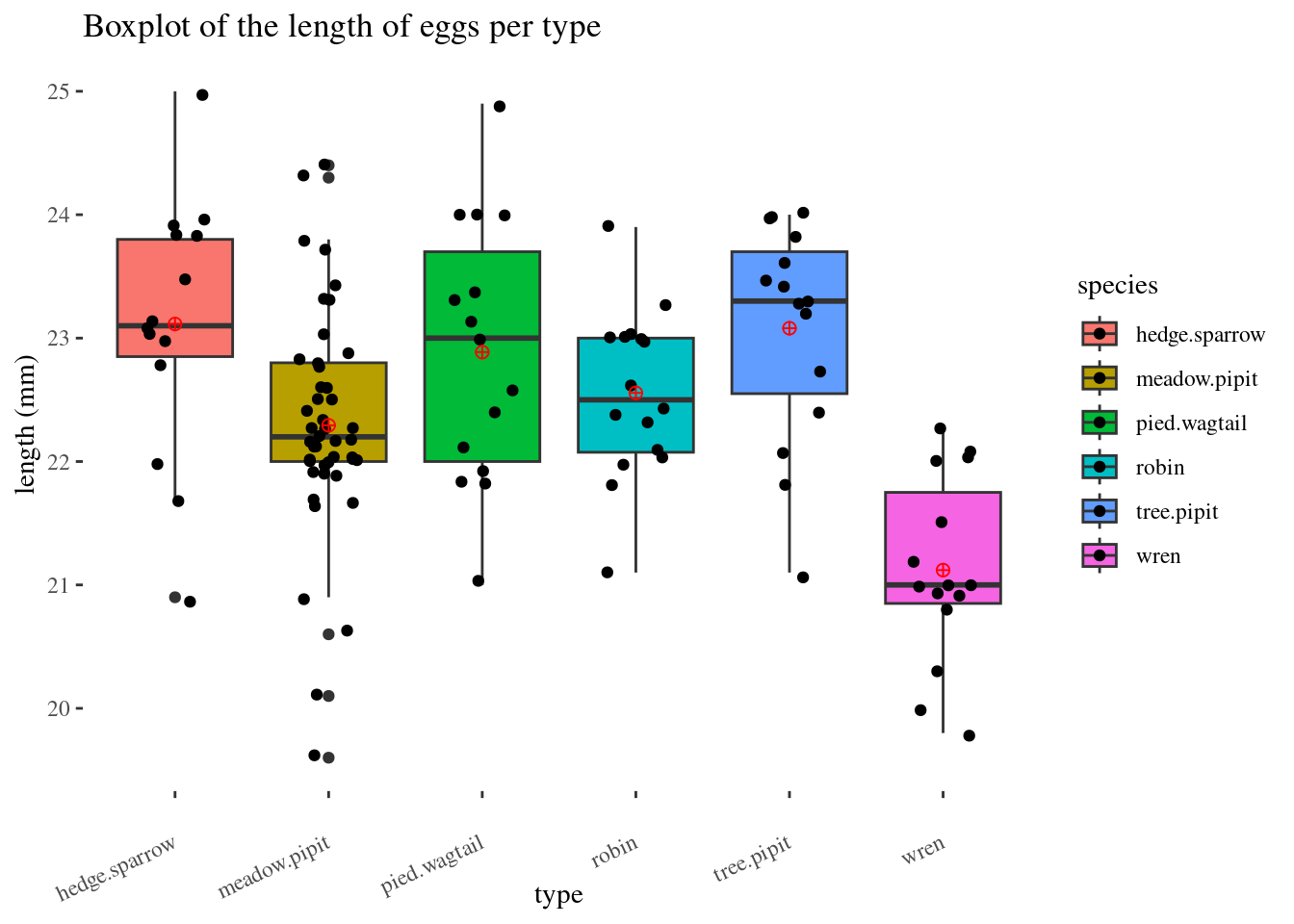
Cuckoo %>%
  ggplot(aes(x=species,y=length,fill=species)) +
  theme_bw() +
  geom_boxplot() +
  geom_jitter(width = 0.2) +
  labs(title ="Boxplot of the length of eggs per type", 
       y = "length (mm)",
       x = "type") + 
  stat_summary(fun=mean, geom="point", shape=10, 
               size=2, color="red", fill="black") +
  ggthemes::theme_tufte() +
  theme(axis.text.x = element_text(angle = 25, hjust = 1, vjust = 0.5))

Check Assumptions

\[H_0: \text{The mean egg length is equal between the different bird tpyes.}\] \[H_a: \text{The mean egg length for at least one bird type is different }\]

Make sure that all assumptions for ANOVA are met:

The data (length) must be normally distributed (in all groups)
The variability within all groups is similar

Approximate normality in groups

QQ-plot
Code

Cuckoo %>% 
  ggplot(aes(sample=length)) + 
  geom_qq() + 
  geom_qq_line() + 
  facet_grid(~species) +  
  theme(strip.text.x = element_text(size = 6)) +
  theme_bw()

Fitting ANOVA

library(broom)
fit_anova <- aov(length~species, Cuckoo)
knitr::kable(tidy(fit_anova))

term	df	sumsq	meansq	statistic	p.value
species	5	42.81015	8.5620298	10.44934	0
Residuals	114	93.40985	0.8193847	NA	NA

Since the p-value is very small, at the significance level of \(5\%\), we have sufficient evidence to conclude that the mean egg length for at least one bird type is different from the mean egg length in at least one other bird type.

But which of the species are different?

Inference after ANOVA

Compute a CI for any \(\mu_i\)

\[\bar{x}_i \pm t^{*} \frac{s_i}{\sqrt{n_i}}\]

BUT after ANOVA, estimate any \(\sigma\) with the pooled standard deviation:

\[\bar{x}_i \pm t^{*}\frac{\sqrt{MSE}}{\sqrt{n_i}}\]

the corresponding df=n-k

Cuckoo Eggs

Find a 95% confidence interval for the mean cuckoo egg length in European robin nests (Type = 4).

MSE <- 0.8193847
knitr::kable(tidy(fit_anova))

term	df	sumsq	meansq	statistic	p.value
species	5	42.81015	8.5620298	10.44934	0
Residuals	114	93.40985	0.8193847	NA	NA

species	mean	sd	n
hedge.sparrow	23.11429	1.0494373	14
meadow.pipit	22.29333	0.9195849	45
pied.wagtail	22.88667	1.0722917	15
robin	22.55625	0.6821229	16
tree.pipit	23.08000	0.8800974	15
wren	21.12000	0.7542262	15

\[\bar{x}_i \pm t^{*}\frac{\sqrt{MSE}}{\sqrt{n_i}}, \text{ df = n-k }\]

Inference after ANOVA

\[H_0: \mu_i = \mu_j \text{ vs. } H_a: \mu_i \neq \mu_j\]

Compute a CI for \(\mu_i - \mu_j\)

\[(\bar{x}_i - \bar{x}_j) \pm t^{*} \sqrt{\frac{s_i^2}{n_i} + \frac{s_j^2}{n_j}}\]

Use the usual procedures except estimate any \(\sigma\) with the pooled standard deviation: \(\sqrt{MSE}\) and use the error degrees of freedom, df=n-k, for any t-values \[(\bar{x}_i - \bar{x}_j) \pm t^{*} \sqrt{MSE \left(\frac{1}{n_i} + \frac{1}{n_j}\right)}\]

Cuckoo Eggs

Find a 95% CI for the difference in mean egg length between European robin(type = 4) and Eurasian wren (type = 6) nests.

term	df	sumsq	meansq	statistic	p.value
species	5	42.81015	8.5620298	10.44934	0
Residuals	114	93.40985	0.8193847	NA	NA

\[\begin{align*} (22.556 - 21.120) \pm & 1.981 \cdot \sqrt{0.8194\left(\frac{1}{16} + \frac{1}{15} \right)} \\ &= (0.792, 2.081) \end{align*}\]

species	mean	sd	n
hedge.sparrow	23.11429	1.0494373	14
meadow.pipit	22.29333	0.9195849	45
pied.wagtail	22.88667	1.0722917	15
robin	22.55625	0.6821229	16
tree.pipit	23.08000	0.8800974	15
wren	21.12000	0.7542262	15

MSE <- 0.8193847
(stat[4,2] - stat[6,2]) + c(-1,1)* (qt(1-0.05/2, df=114))* sqrt(MSE*(1/stat[4,4] + 1/stat[6,4]))

[1] 0.7917811 2.0807189

Why is it important that the interval contains only positive values?

Cuckoo Eggs

Find a 95% CI for the difference in mean egg length between Pied Wagtail (type = 3) and European robin (type = 4) nests.

term	df	sumsq	meansq	statistic	p.value
species	5	42.81015	8.5620298	10.44934	0
Residuals	114	93.40985	0.8193847	NA	NA

\[\begin{align*} (22.887 - 22.556) \pm & 1.981\cdot \sqrt{0.8194\left(\frac{1}{15} + \frac{1}{16} \right)}\\ &= (-0.314, 0.975) \end{align*}\]

species	mean	sd	n
hedge.sparrow	23.11429	1.0494373	14
meadow.pipit	22.29333	0.9195849	45
pied.wagtail	22.88667	1.0722917	15
robin	22.55625	0.6821229	16
tree.pipit	23.08000	0.8800974	15
wren	21.12000	0.7542262	15

(stat[3,2] - stat[4,2]) + c(-1,1)* (qt(1-0.05/2, df=114))*sqrt(MSE*(1/stat[3,4] + 1/stat[4,4]))

[1] -0.3140522  0.9748855

What does it mean if the interval contains 0?

Mutiple Comparisons

Often, doing pairwise comparisons after ANOVA involves many tests

e.g. \(k\) groups/categories,then we have \(\frac{k(k-1)}{2}\) comparisons
\(k=6\) bird species then 15 pairwise tests.

Mutiple Comparisons

If each test has an \(\alpha\) chance of a Type I error (finding a difference between a pair that aren’t different), the overall Type I error rate can be much higher.

Use a smaller \(\alpha\) for each pairwise test (Bonferroni)

\(\alpha^{*} = \frac{\alpha}{k}\)
e.g \(\alpha = 0.05\) and \(k = 6\), then \(\alpha^{*} = 0.05/6 = 0.0083\)

Cuckoo Eggs

Which means are “different” at a \(5\%\) significance level?

pairwise.t.test(Cuckoo$length, Cuckoo$species, p.adjust.method =  "bonferroni")


    Pairwise comparisons using t tests with pooled SD 

data:  Cuckoo$length and Cuckoo$species 

             hedge.sparrow meadow.pipit pied.wagtail robin   tree.pipit
meadow.pipit 0.05554       -            -            -       -         
pied.wagtail 1.00000       0.44898      -            -       -         
robin        1.00000       1.00000      1.00000      -       -         
tree.pipit   1.00000       0.06426      1.00000      1.00000 -         
wren         5e-07         0.00045      7e-06        0.00035 5e-07     

P value adjustment method: bonferroni

Please download the Class-Activity-25 template from moodle and go to class helper web page

30:00

Post-ANOVA

Post-ANOVA

ANOVA for Difference in Means

Cuckoo Birds

Cuckoo Dataset

ANOVA: Numerical summary

Side-by-side Boxplot

Check Assumptions

Approximate normality in groups

Fitting ANOVA

Inference after ANOVA

Cuckoo Eggs

Inference after ANOVA

Cuckoo Eggs

Cuckoo Eggs

Mutiple Comparisons

Mutiple Comparisons

Cuckoo Eggs

Group Activity 1