| Year | Gender | Smoke | Exercise | TV | Height | Weight | Siblings | BirthOrder | GPA | Pulse |
|---|---|---|---|---|---|---|---|---|---|---|
| Senior | M | No | 10 | 1 | 71 | 180 | 4 | 4 | 3.13 | 54 |
| Sophomore | F | Yes | 4 | 7 | 66 | 120 | 2 | 2 | 2.50 | 66 |
| FirstYear | M | No | 14 | 5 | 72 | 208 | 2 | 1 | 2.55 | 130 |
| Junior | M | No | 3 | 1 | 63 | 110 | 1 | 1 | 3.10 | 78 |
| Sophomore | F | No | 3 | 3 | 65 | 150 | 1 | 1 | 2.70 | 40 |
| Sophomore | F | No | 5 | 4 | 65 | 114 | 2 | 2 | 3.20 | 80 |
| FirstYear | F | No | 10 | 10 | 66 | 128 | 1 | 1 | 2.77 | 94 |
| Sophomore | M | No | 13 | 8 | 74 | 235 | 1 | 1 | 3.30 | 77 |
| Junior | F | No | 3 | 6 | 61 | NA | 2 | 2 | 2.80 | 60 |
| FirstYear | F | No | 12 | 1 | 60 | 115 | 7 | 8 | 3.70 | 94 |
Describing Variables
STAT 120
Student Survey
Dataset on 362 responses to a student survey given at one college
Distribution
In the given dataset, there are multiple variables (such as Gender, Smoke, Exercise, Height, Weight, etc.) for different students across various academic years.
Knowing the distribution of each variable can help us identify relationships, trends, and potential anomalies in the data.
Understanding distribution
Understanding the distribution of the data is useful for several reasons:
- Descriptive analysis:
- Data quality:
- Assumption checking:
- Interpretation of results:
- Visualization:
Distribution
“The distribution of the variable Y”
- describes its center, variability and shape
- use both numbers and graphics
Center: Mean or Average
Mean: average value in a sample or population
- \(\bar{y} = \dfrac{\sum_{i=1}^ny_i}{n}\) is an average of \(n\) values \(y_i\) in a sample
- \(\mu\) is an average value of \(y\) in a population
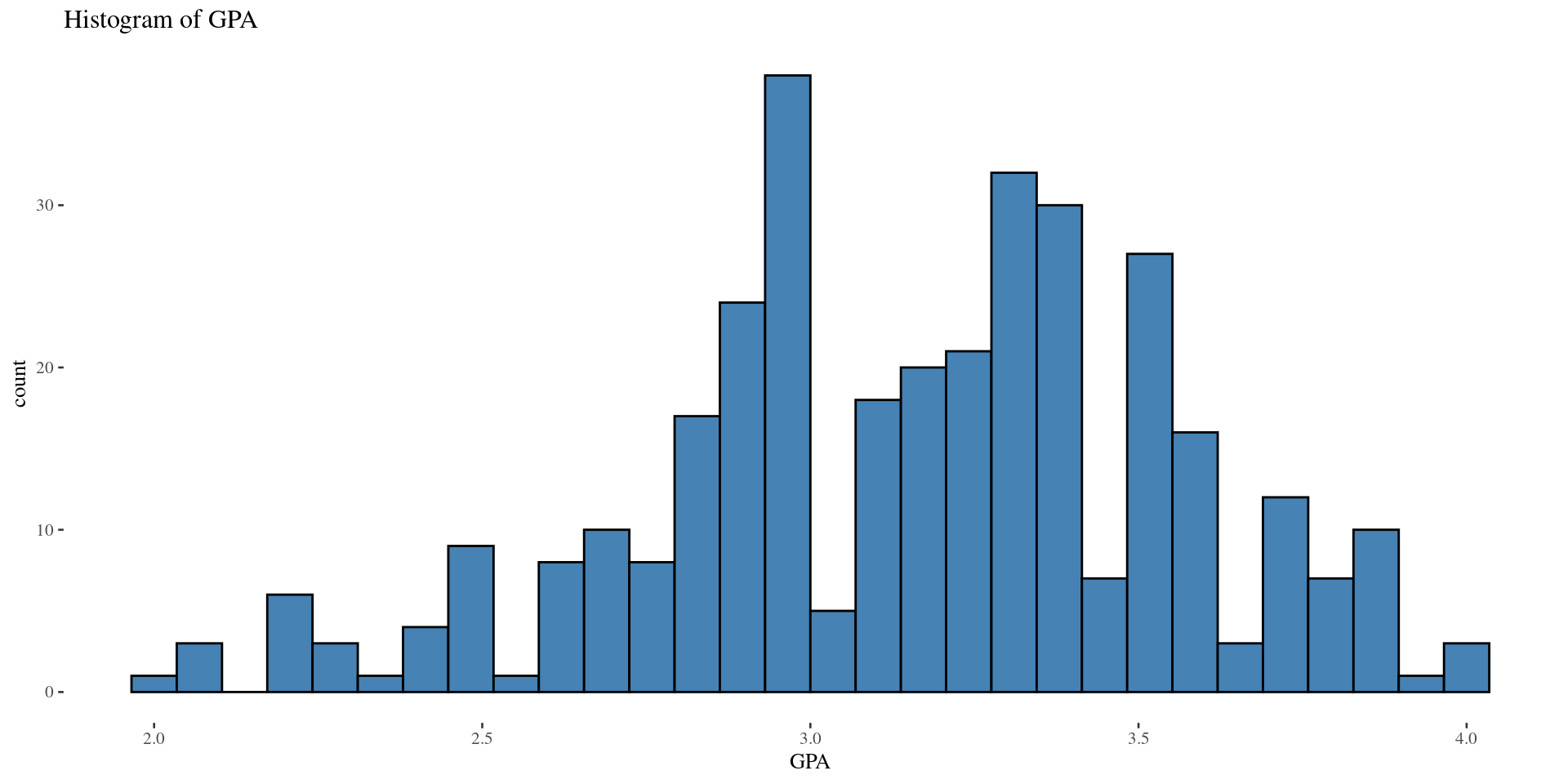
Student Survey
Center: Median
Median: the middle value when the data are ordered
- The median splits the data in half
- \(m\) is the median value in a sample
- \(M\) is the median value in a population
The median pulse rate for this sample of students is \(m = 70\) beats per minute.
Variability: Standard Deviation
Standard Devation (SD): average deviation from center in a sample or population
- \(s = \sqrt{ \dfrac{\sum_{i=1}^n(y_i - \overline{y})^2}{n-1}}\) is the SD of \(n\) values \(y_i\) in a sample
- \(\sigma\) is the SD of values of \(y\) in a population
The SD of pulse rates for this sample of students is \(s = 12.2\) beats per minute. The “average” deviation of individual pulse rates around the mean value is about 12.2 beats per minute.
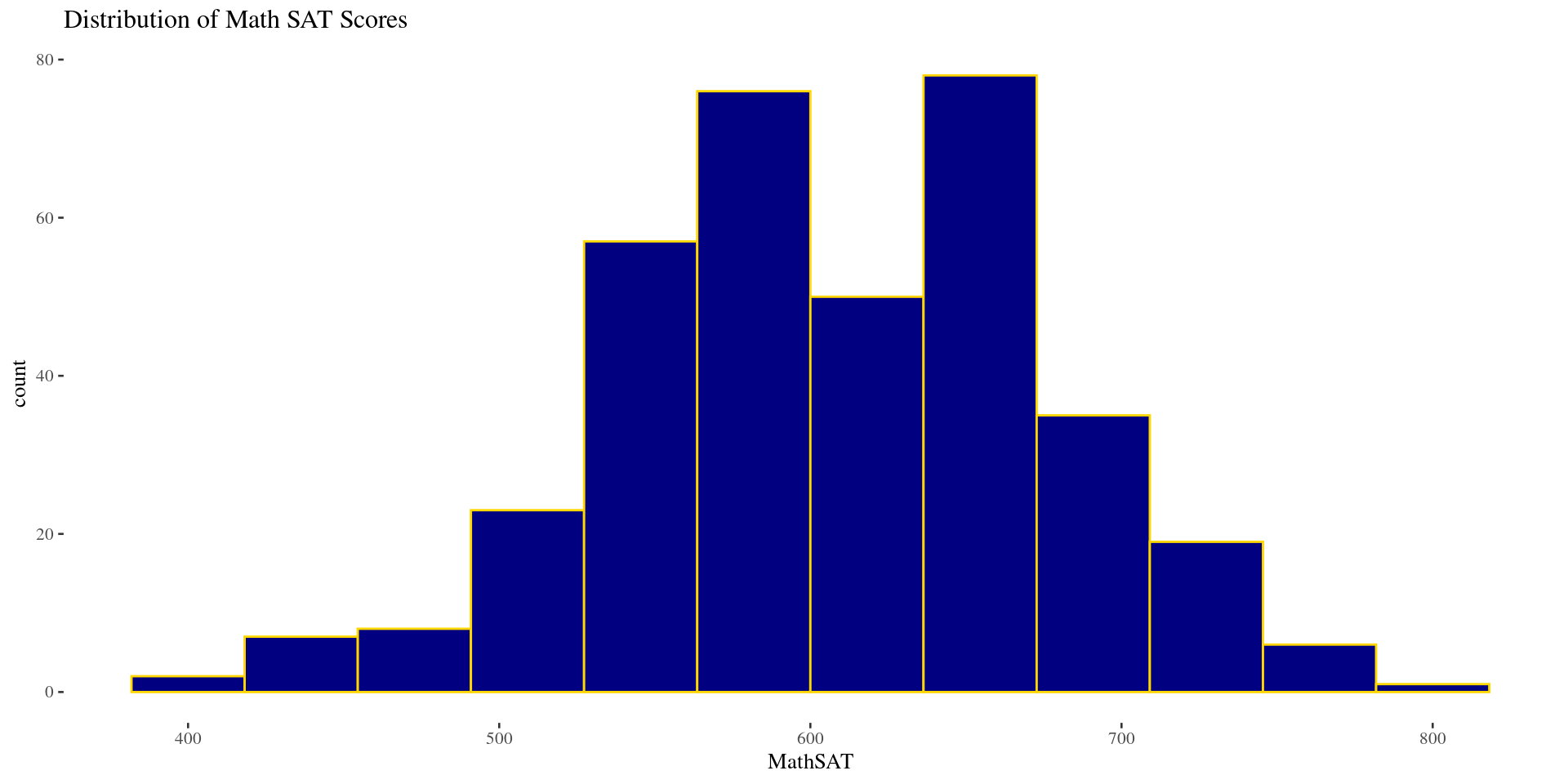
Shape: histogram
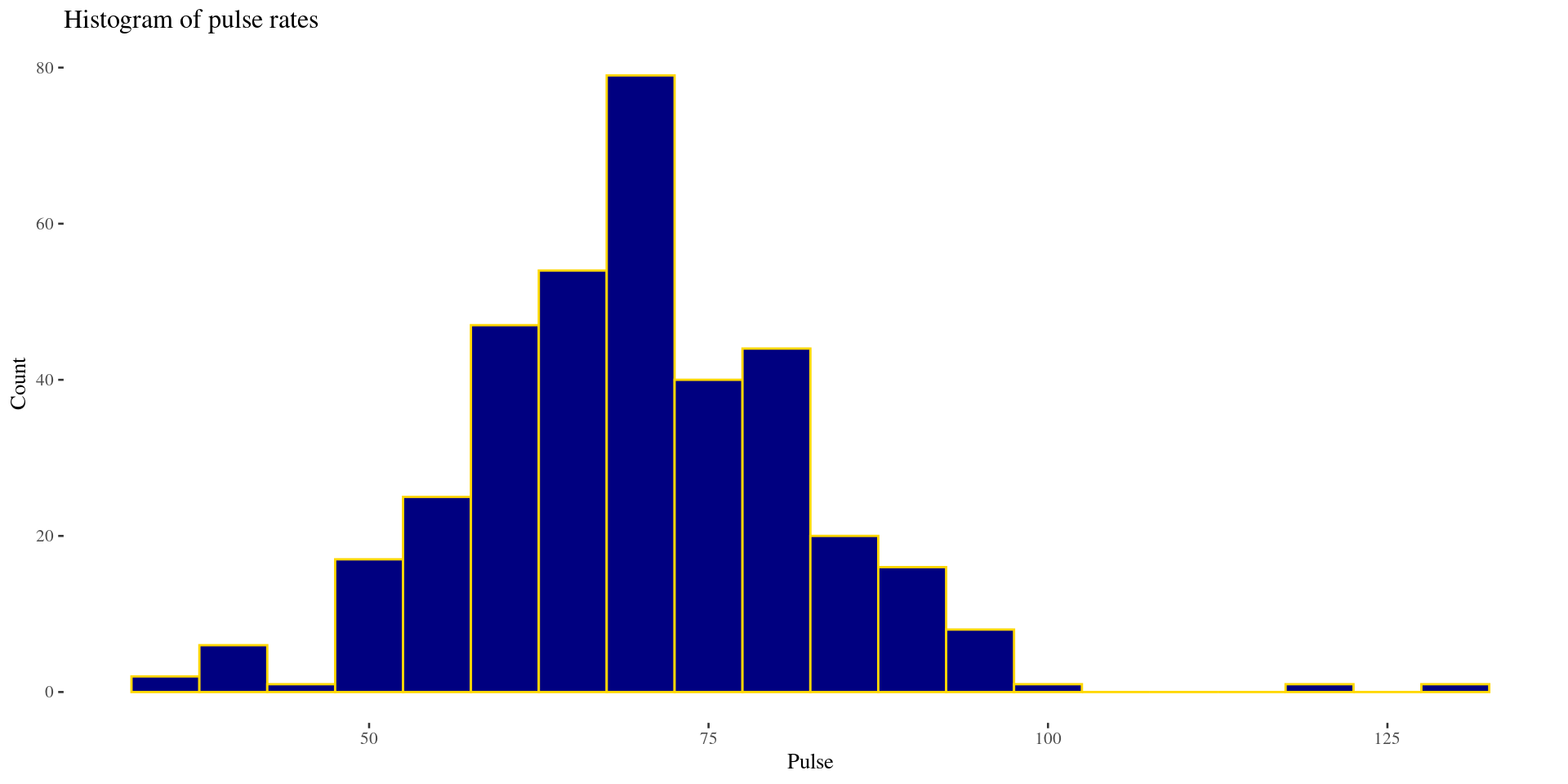
Shape: histogram
- Histogram: aggregates values into bins and counts how many cases fall into each bin
- Pulse rates are symmetrically distributed around a rate of about 70 beats per minute.
- Symmetric distributions are “centered” around a mean and median that are roughly the same in value.
Shape and Stats
- Mean and standard deviation are good summary stats of a symmetric distribution.
- Similar variation to the left and right of the mean so one measure of SD is fine.
Shape: data distribution
If a distribution of data is approximately bell-shaped, about 95% of the data should fall within two standard deviations of the sample mean.
- for a sample: 95% of values between \(\bar{y} - 2s\) and \(\bar{y} + 2s\)
- for a population: 95% of values between \(\mu - 2\sigma\) and \(\mu + 2\sigma\)
Bell-shaped distribution
Standardizing data: z-score
The z-score of a data value, x, tells us how many standard deviations the value is above or below the mean:
\[z = \dfrac{x - \text{mean}}{\text{SD}}\]
- E.g. if a value \(x\) has \(z=-1.5\) then the value \(x\) is 1.5 standard deviations below the mean.
Question: If we standardize all values in a bell-shaped distribution, 95% of all z-scores fall between what values?
Shape: Left Skew \(\&\) Right Skew (Histograms)
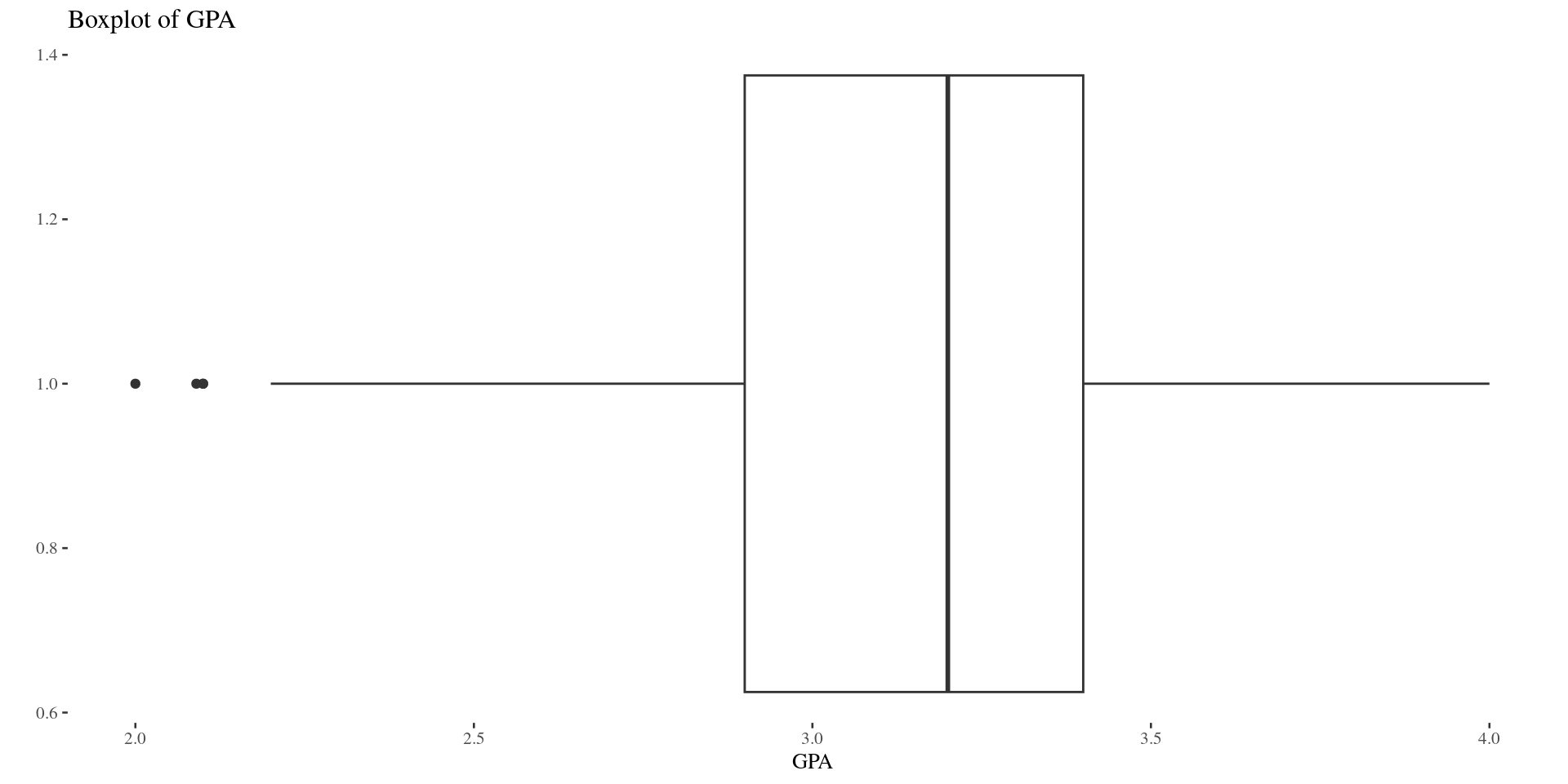
Shape: Left Skew \(\&\) Right Skew (Boxplots)
Shape: boxplots
Boxplots: A graphical representation of the distribution of a dataset, showing the median, quartiles, and outliers.
- Box: Represents the interquartile range (IQR) between the 1st quartile (Q1) and the 3rd quartile (Q3)
- Median: The middle value of the dataset, represented by a line inside the box
- Whiskers: Extend from the box to the minimum and maximum data points within 1.5 times the IQR
- Outliers: Data points outside of the whiskers, often represented as individual points
Shape: boxplots
Symmetry: If the median is roughly centered within the box, and the whiskers are of similar length, the distribution is likely symmetric.
Skewness:
- Left-skewed: The median is closer to the upper quartile (Q3), and the left whisker is longer than the right whisker.
- Right-skewed: The median is closer to the lower quartile (Q1), and the right whisker is longer than the left whisker.
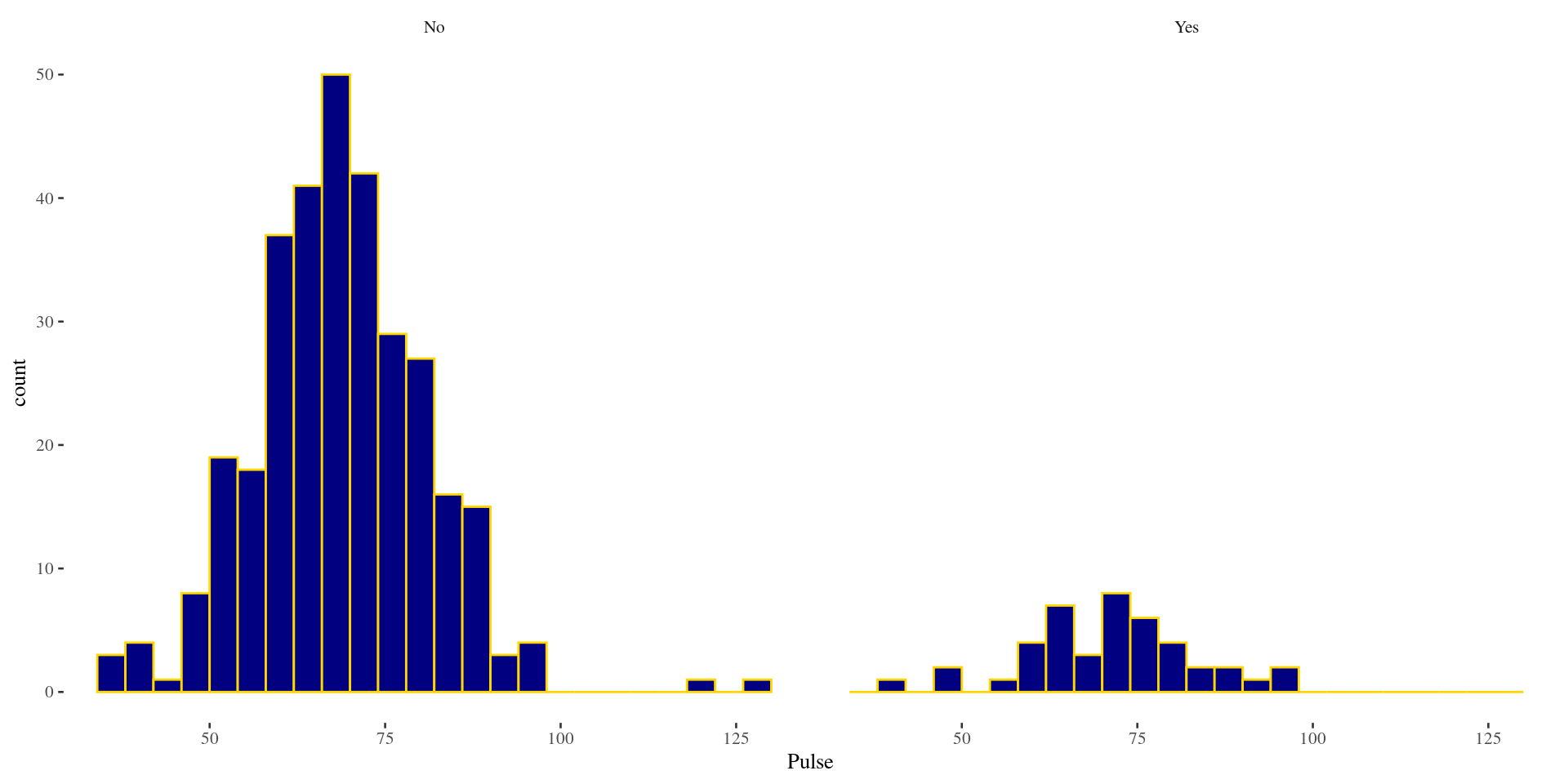
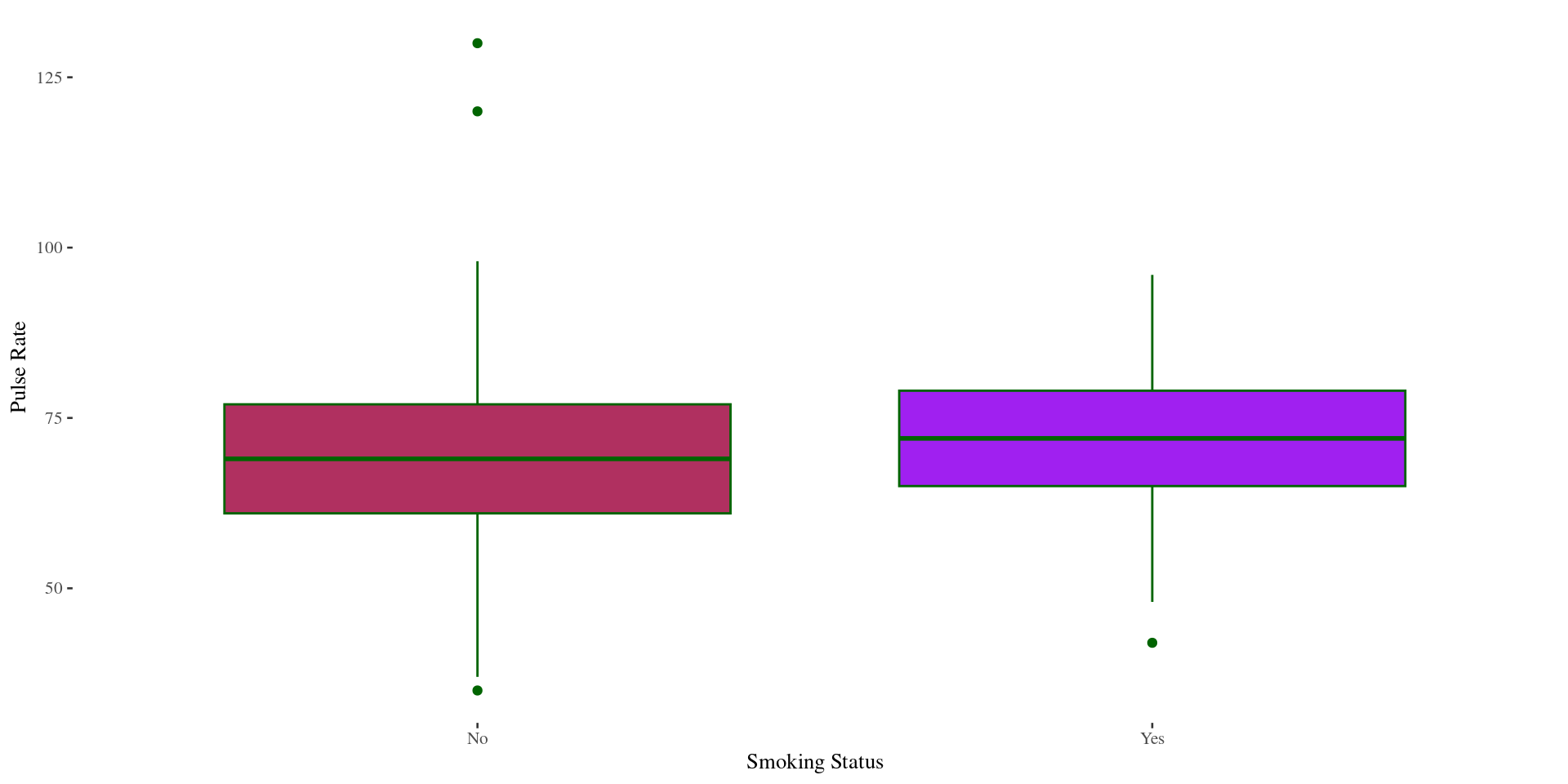
Adding a categorical variable: stats
Use group_by() and summarise() to get summary statistics using dplyr package to compare distributions across different levels of a categorical variable
library(dplyr)
survey %>%
group_by(Smoke) %>%
summarise(Min = min(Pulse),
Q1 = quantile(Pulse, 0.25),
Median = median(Pulse),
Mean = mean(Pulse),
Q3 = quantile(Pulse, 0.75),
Max = max(Pulse),
SD = sd(Pulse),
N = n()) %>%
knitr::kable(caption = "Summary Stats of Smoke Categories")| Smoke | Min | Q1 | Median | Mean | Q3 | Max | SD | N |
|---|---|---|---|---|---|---|---|---|
| No | 35 | 61 | 69 | 69.27273 | 77 | 130 | 12.26096 | 319 |
| Yes | 42 | 65 | 72 | 71.81395 | 79 | 96 | 11.67671 | 43 |
Smoker have a slightly higher mean pulse rate than non-smokers (71.8 vs. 69.3).
Histogram
Boxplots
Group Activity 1

- Please download the Class-Activity-5 template from moodle and go to class helper web page
30:00