Sampling Distribution and Bootstrap

STAT 120

Bastola

Statistical Inference

Statistical inference is the process of drawing conclusions about the entire population based on information in a sample.



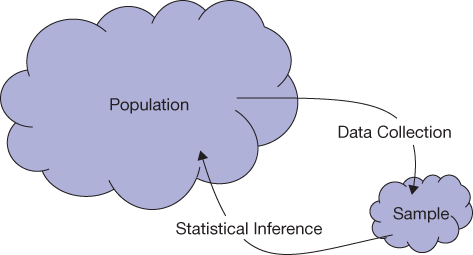
Statistical Inference

Motivating Example 1


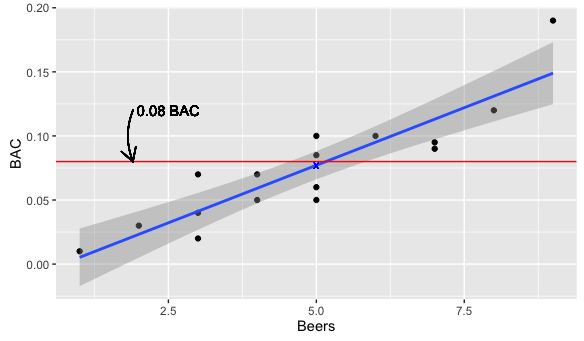
Regression line of Bood alcohol content (BAC) Vs. number of beers

Can you drink 5 beers and stay under the 0.08 limit?

Motivating Example 2


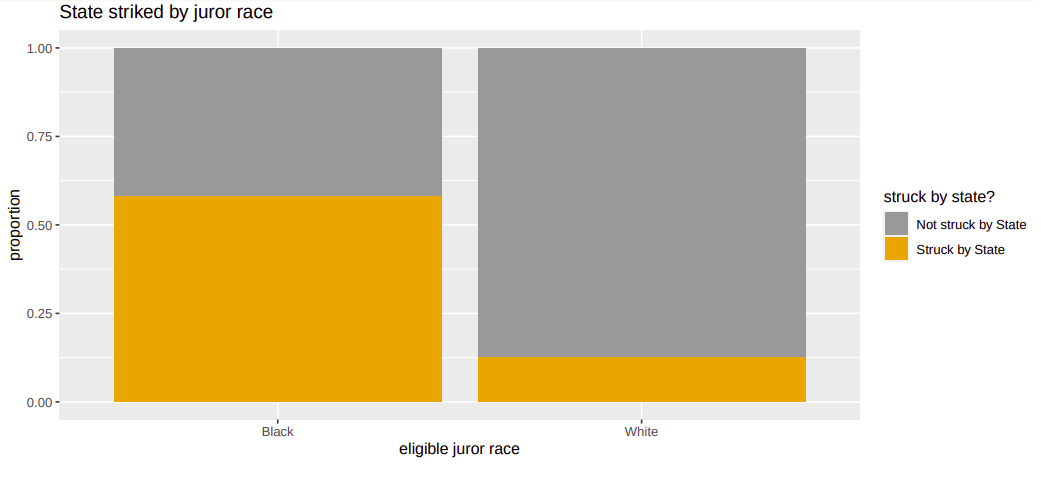
Striking rates by race

Do the observed differences in strike rates between black and white eligible jurors indicate a potential bias, or are the differences just due to chance?

Statistic and Parameter

  • A parameter is a number that describes some aspect of a population.
  • A statistic is a number that is computed from data in a sample.
  Parameter Statistic
Mean \(\mu\) \(\bar{x}\)
Proportion \(p\) \(\hat{p}\)
Std. Dev. \(\sigma\) \(s\)
Correlation \(\rho\) \(r\)
Slope \(\beta\) \(b\)

Parameter Vs. Statistic

State whether the quantity described is a parameter or a statistic, and give the correct notation.

  1. Average household income for all houses in the US, using data from the US census


  1. The proportion of all residents in a county who voted in the last presidential election.


  1. The difference in proportion who have ever smoked cigarettes, between a sample of 500 people who are 60 years old and a sample of 200 people who are 25 years old.


Point Estimate (PE)

  • Point estimate is a single value constructed from the sample data
  • Sample statistic can serve as a point estimate for an unknown parameter

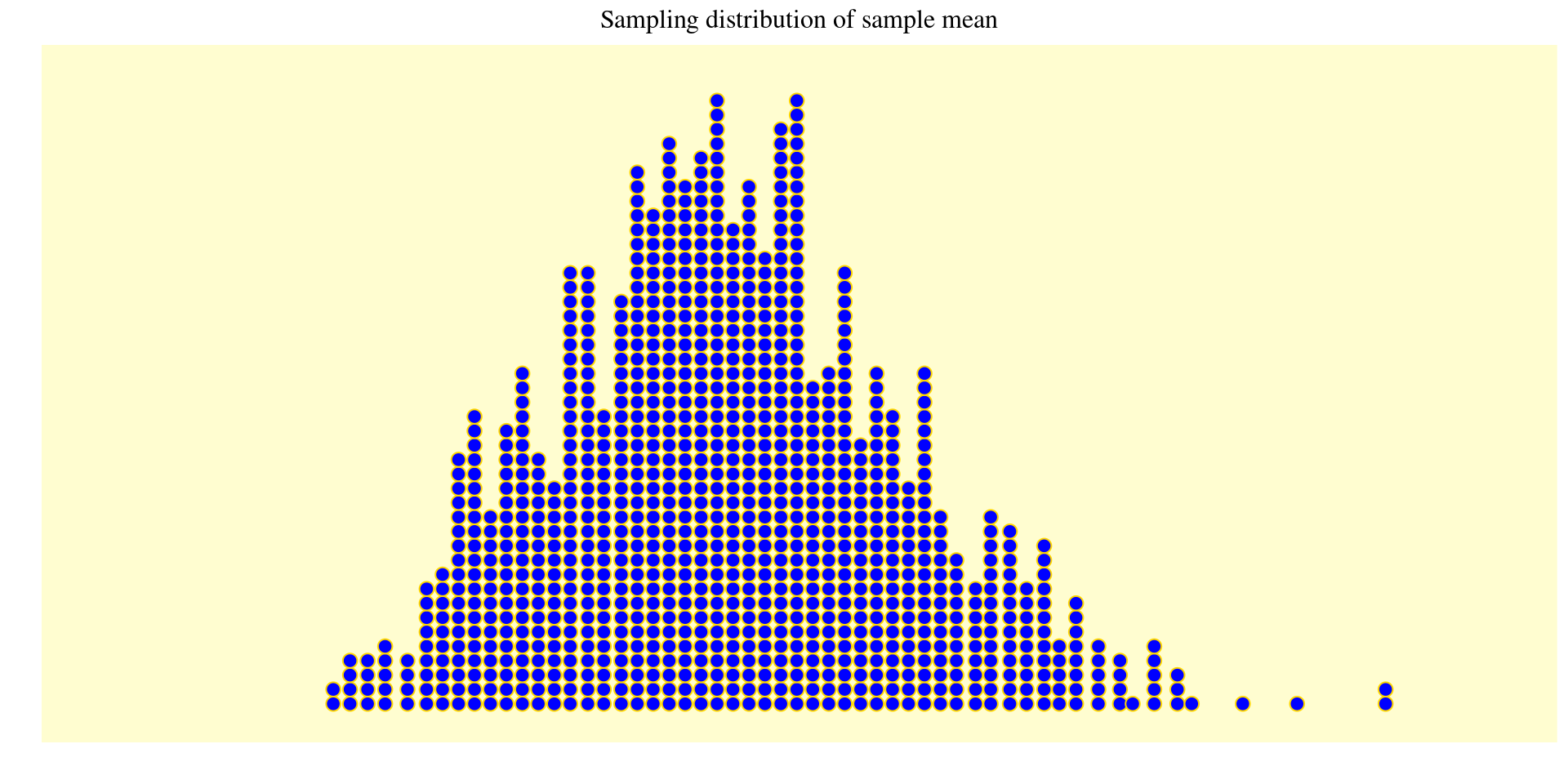
Sampling Distribution

A sampling distribution is the distribution of sample statistics computed for different samples of the same size from the same population.

  • Sample statistics varies from sample to sample
  • Sampling distribution gives us an idea of the variation

Center and Shape

Center: If samples are randomly selected, the sampling distribution will be centered around the population parameter.

Shape: For most of the statistics we consider, if the sample size is large enough the sampling distribution will be symmetric and bell-shaped.

Standard Error

Uncertainty in point estimates measured by the standard error (SE)

  • The standard error of a statistic is the standard deviation of the sampling distribution
  • The standard error measures how much the statistic varies from sample to sample

 Group Activity 1




A Short demo on Sampling distribution

05:00

Recall: Gettysburg Address

The standard error for the average word size in a random sample of 10 words is closest to

  1. 0.5
  2. 0.7
  3. 1.0
  4. 1.5


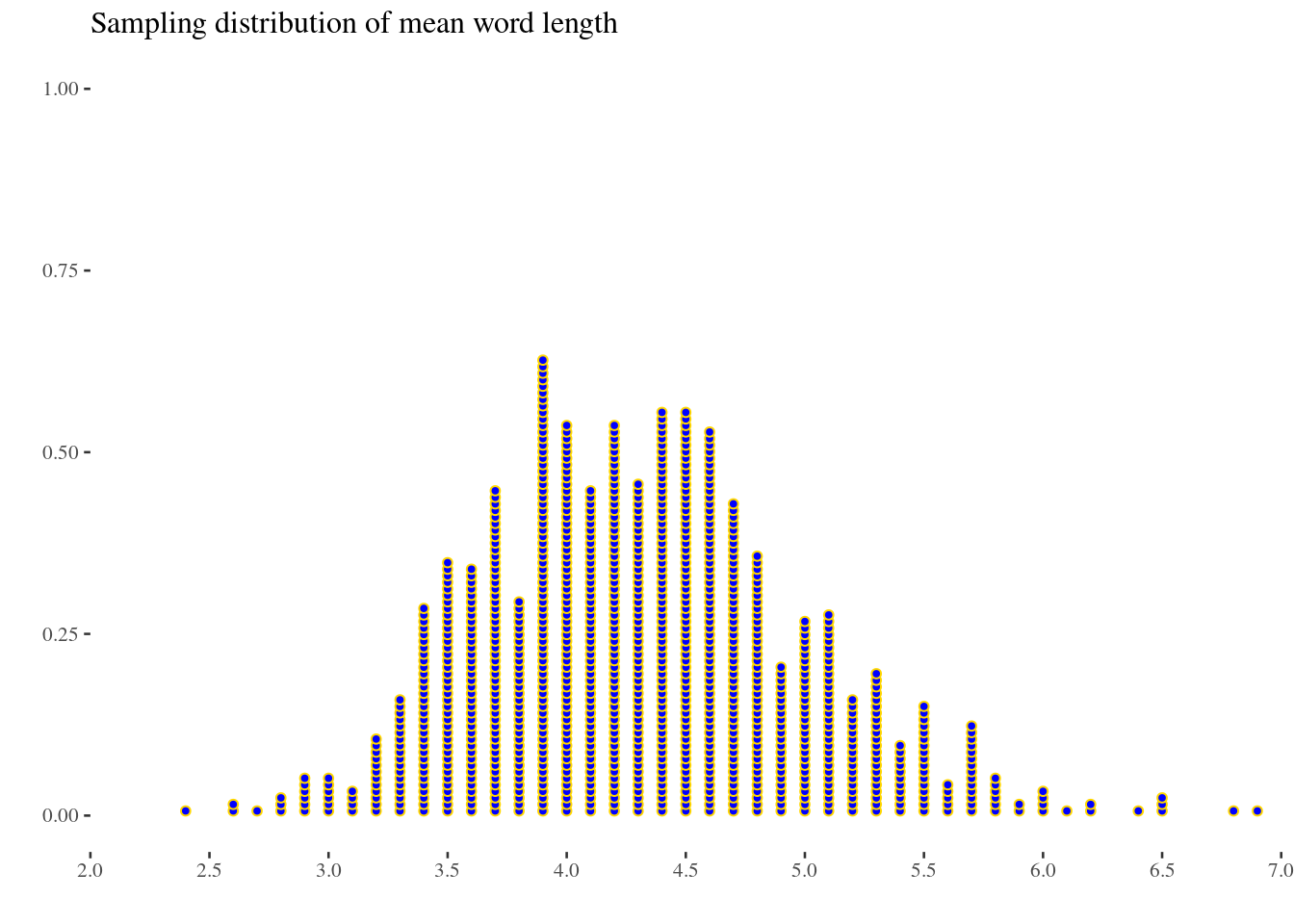
Sample Size Matters!


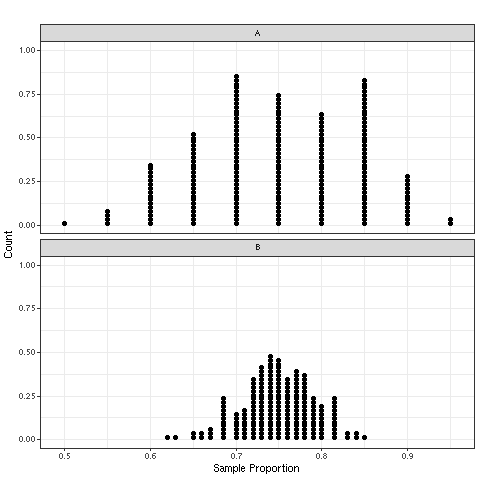
Sample Size Matters!

  • As the sample size increases, the variability (SE) of the sample statistics tends to decrease.
  • Smaller SE means the sample statistics tend to be closer to the true population parameter value!

Sample Size vs. Simulation size

Sample size (n) = how many individuals are in the sample used to compute our stat?

Simulation size (N) = how many random samples did we take from the population to simulate the sampling distribution of our stat?

  • The SE of your stat gets smaller as \(n\) get bigger.

  • Once you’ve simulated a couple \(100\) samples, the shape/center/spread of the sampling distribution should remain about the same as you increase the simulation size.

Random Vs. Non-random

Samples of size 5 are taken from a large population with population mean 8, and the sampling distributions for the sample means are shown. Dataset A (top) and Dataset B (bottom) were collected using different sampling methods. Which dataset (A or B) used random sampling?


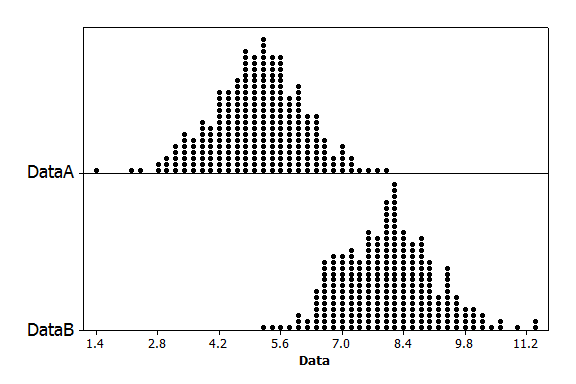
Random Vs. non-random data distribution

Bootstrap

Bootstrap: Sample with replacement from the original sample, using the same sample size.


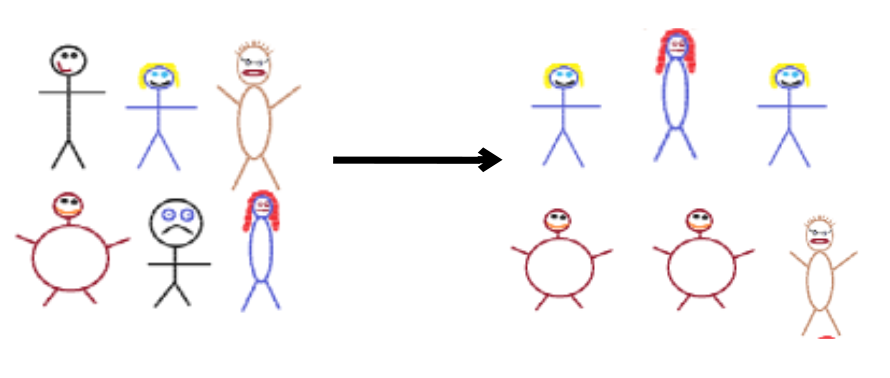
Original sample (left) to bootstrap sample (right)

Bootstrap


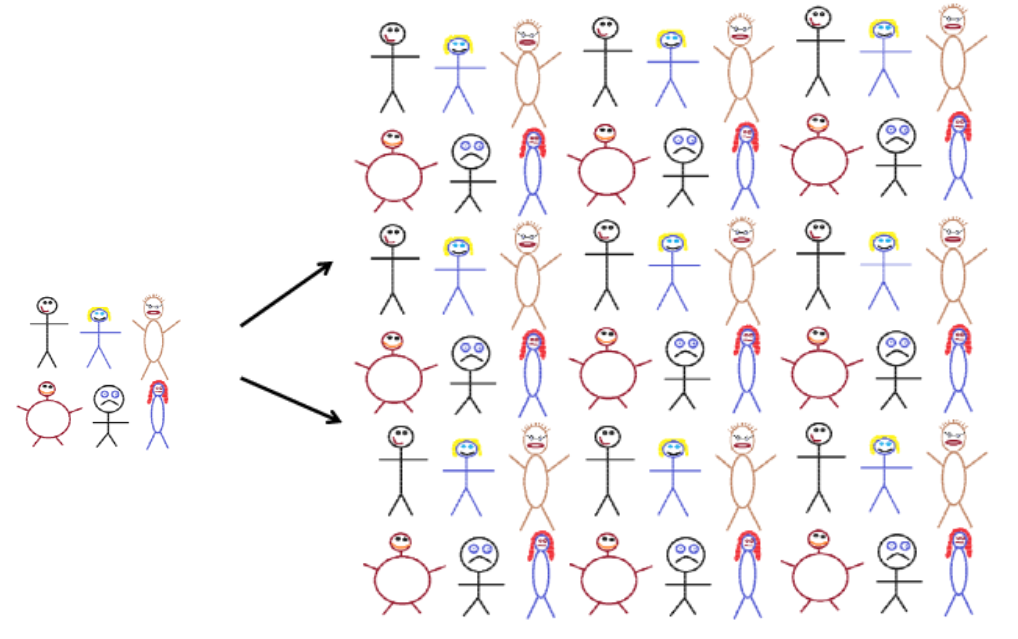
Original sample (left) to population (right)

Creating a bootstrap sample is the same as using the data simulate a “population” that contains an infinite number of copies of the data.

Bootstrap Sampling in R

  • resample a set of observations with replacement
  • same data points can appear multiple times
  Data
Original sample \(x_1, x_2, ..., x_n\)
Resample \(x_1^*, x_2^*, ..., x_n^*\) 
# R-code
boot <- sample(x, size, replace = TRUE)

Bootstrap Steps



  1. Generate a bootstrap sample.

  2. Compute the statistic of interest for your bootstrap sample.

  3. Repeat steps (1) – (2) many times. Plot the distribution of all your bootstrap statistics

This is the bootstrap distribution!

Statkey Demo Page for Bootstrap

 Group Activity 2


20:00