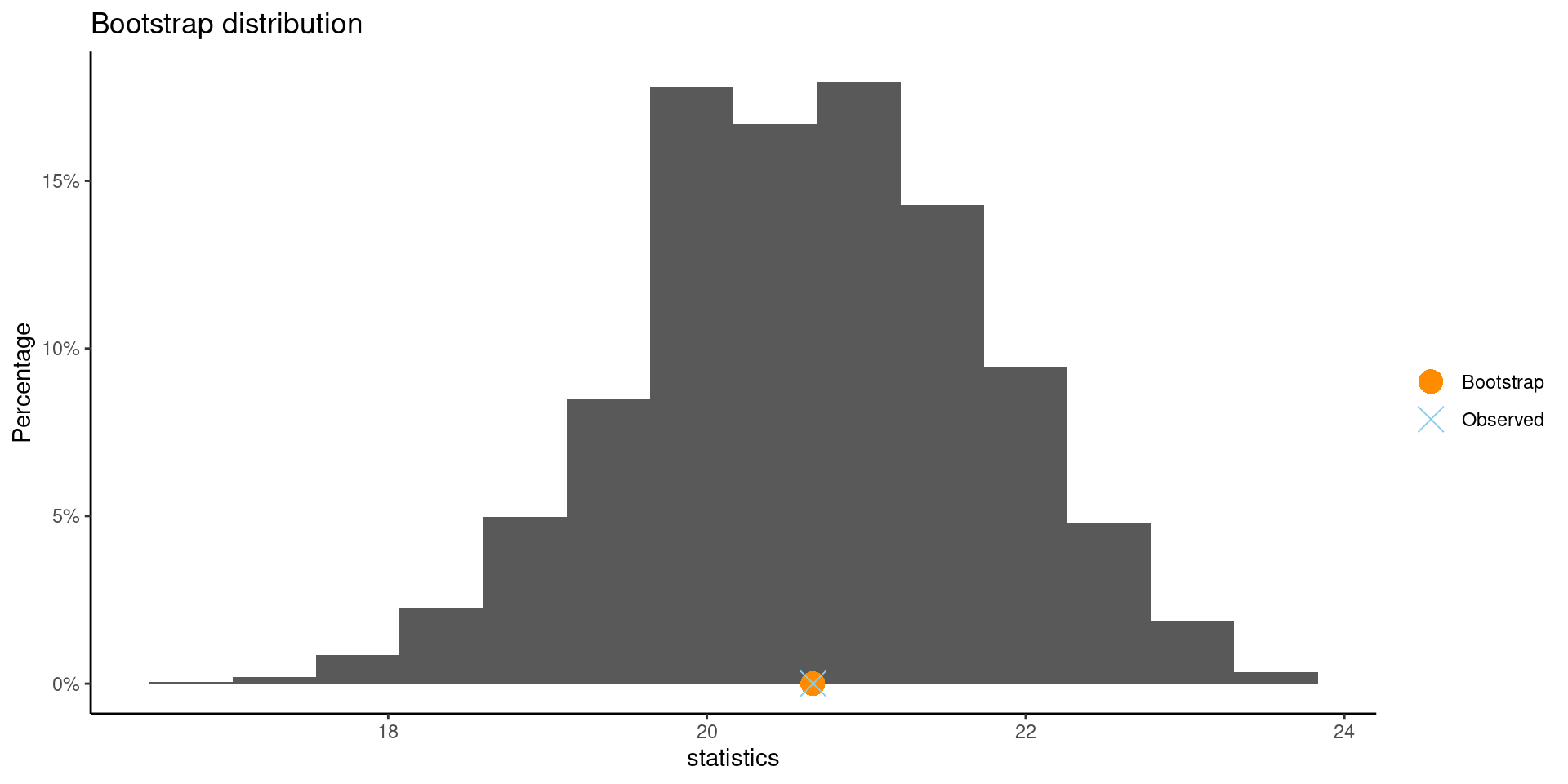
** Bootstrap interval for mean
Observed X : 20.66667
Mean of bootstrap distribution: 20.66403
Standard error of bootstrap distribution: 1.09819
Bootstrap percentile interval
2.5% 97.5%
18.50000 22.66667
*--------------*
STAT 120
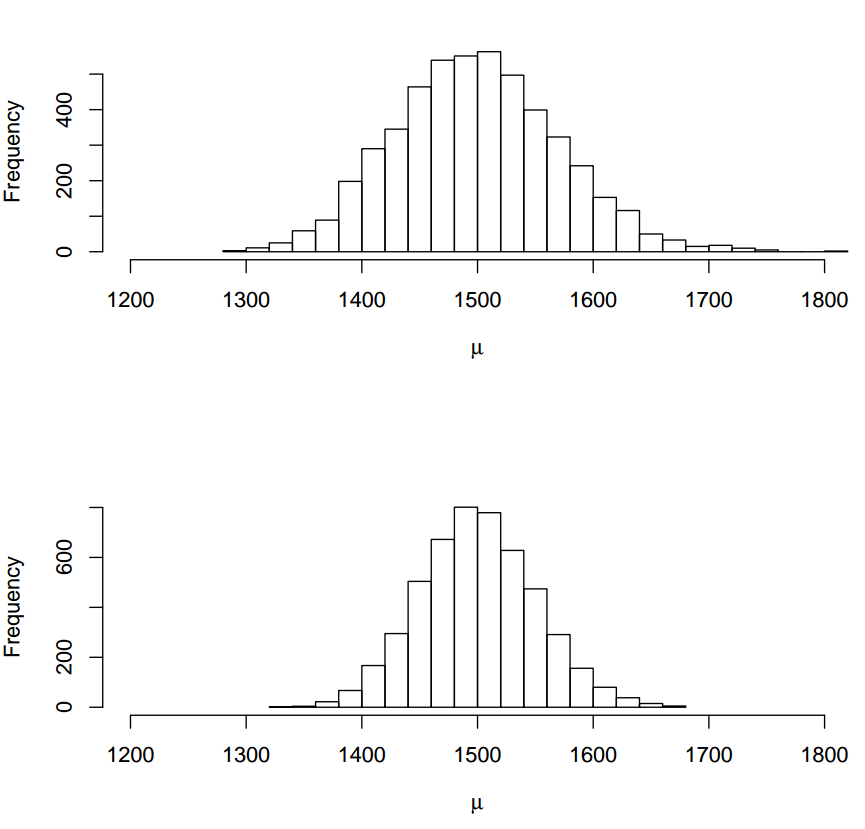
The higher the standard error of a statistic, the \(\ldots \ldots\) the uncertainty surrounding the statistic.
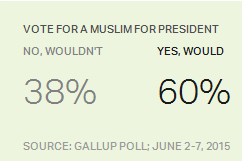
How accurate is an estimate of \(60\%\)?

Link to the Gallup poll
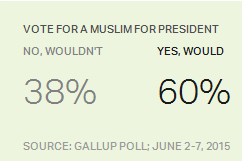
" \(\ldots\) the margin of sampling error is \(\pm\) 3 percentage points at the \(95\%\) confidence level.”
The margin of error measures how accurate a point estimate is likely to be in estimating a parameter.
To determine the margin of error, we can use the statistic’s sampling distribution and standard error
If the sampling distribution is relatively symmetric and bell-shaped, a \(95\%\) confidence interval can be estimated using \[\mathbf{statistic} \pm 2 \times \mathbf{SE}\]
Let’s all go to Statkey web app.

A bootstrap distribution is the distribution of many bootstrap statistics.
** Bootstrap interval for mean
Observed X : 20.66667
Mean of bootstrap distribution: 20.66403
Standard error of bootstrap distribution: 1.09819
Bootstrap percentile interval
2.5% 97.5%
18.50000 22.66667
*--------------*

30:00