Practice Problems 19

Problem 1: Florida Lakes pH

The textbook dataset FloridaLakes contains data on 53 lakes in Florida. We want to know if the average pH of lakes in Florida is different from a neutral value of 7.

lakes <- read.csv("http://www.lock5stat.com/datasets1e/FloridaLakes.csv")
head(lakes)

  ID         Lake Alkalinity  pH Calcium Chlorophyll AvgMercury NumSamples
1  1    Alligator        5.9 6.1     3.0         0.7       1.23          5
2  2        Annie        3.5 5.1     1.9         3.2       1.33          7
3  3       Apopka      116.0 9.1    44.1       128.3       0.04          6
4  4 Blue Cypress       39.4 6.9    16.4         3.5       0.44         12
5  5        Brick        2.5 4.6     2.9         1.8       1.20         12
6  6       Bryant       19.6 7.3     4.5        44.1       0.27         14
  MinMercury MaxMercury ThreeYrStdMercury AgeData
1       0.85       1.43              1.53       1
2       0.92       1.90              1.33       0
3       0.04       0.06              0.04       0
4       0.13       0.84              0.44       0
5       0.69       1.50              1.33       1
6       0.04       0.48              0.25       1

(a) EDA

Always plot your data and get summary stats:

library(ggplot2)
ggplot(lakes, aes(pH)) + geom_histogram(bins=10, fill = "lightblue", color = "gold")

mean(lakes$pH)

[1] 6.590566

sd(lakes$pH)

[1] 1.288449

What are the sample mean and standard deviation? Use appropriate notation.
Can we use t-inference methods with the pH variable?

Click for answer

Answer: The average pH was \(\bar{x} = 6.591\) with a standard deviation of \(s=1.288\). The distribution of pH is symmetric with no outliers, so we can use t-inference methods.

(b) SE for the sample mean

What is the estimated SE for the sample mean?

Click for answer

Answer: The estimated SE for the sample mean is \(SE_{\bar{x}} = 0.1770\).

sd(lakes$pH)/sqrt(53)

[1] 0.1769821

(c) t-test statistic

Using your SE from (b) to compute the t-test statistic for testing if the population mean pH is equal, or not, to 7. Write down your hypotheses then show how the t test statistic is calculated. Interpret this value in context.

Click for answer

Answer: The hypotheses are \(H_0: \mu = 7\) vs \(H_A: \mu \neq 7\). The test stat is

\[ t = \dfrac{6.591 - 7}{1.288/\sqrt{53}} = -2.3134 \]

The observed mean of 6.591 is 2.3 SEs below the hypothesized mean of 7.

(mean(lakes$pH) - 7)/(sd(lakes$pH)/sqrt(53))

[1] -2.31342

(d) One-sample t-test

The function t.test(x, mu=) can be used for a one sample test comparing the sample mean of x to the hypothesized value given to mu=. Here we are testing whether the population mean is equal to 7 or not:

t.test(lakes$pH, mu = 7)


    One Sample t-test

data:  lakes$pH
t = -2.3134, df = 52, p-value = 0.02469
alternative hypothesis: true mean is not equal to 7
95 percent confidence interval:
 6.235425 6.945707
sample estimates:
mean of x 
 6.590566

What is the t test stat given in the output? Verify that it matches your answer to (c), within reasonable rounding error.

Click for answer

Answer: The test stat is -2.31.

What is the p-value for the test? Interpret this value.

Click for answer

Answer: The p-value is 0.025. If the mean pH of all lakes is 7, then we would see a sample mean that is at least 2.31 SEs away from 7 about 2.5% of the time in samples of 53 lakes.

What is your test conclusion?

Click for answer

Answer: There is a statistically significant difference between the observed mean pH of 6.591 and the hypothesized mean of 7 (t=-2.31, df=52, p=0.025).

(e) One-sample t confidence interval

What is the 95% confidence interval for the population mean pH? Interpret this CI.

Click for answer

Answer: We are 95% confident that the mean pH of all lakes in Florida is between 6.24 and 6.95.

(f) `qt` and `pt`

Show how to compute the p-value for your test in (d) using the pt command. Then show how the confidence interval in (e) is computed with a qt value.

Click for answer

Answer: For the two-sided test, the p-value is twice the proportion below the test stat \(t=-2.313\) under a t-distribution with \(df=53-1=52\)

2*pt(-2.313,df=52)

[1] 0.02471195

For a 95% CI, we get the 97.5th percentile from the same t-distribution

qt(.975,52)

[1] 2.006647

Problem 2: Nutrition Study

The dataset NutritionStudy contains data on daily calorie intake and other variables for 315 individuals. We want to know if the average daily calorie intake is different from the recommended 2000 calories.

library(dplyr)
NutritionStudy <- read.csv("https://www.lock5stat.com/datasets2e/NutritionStudy.csv")
glimpse(NutritionStudy)

Rows: 315
Columns: 17
$ ID            <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 1…
$ Age           <int> 64, 76, 38, 40, 72, 40, 65, 58, 35, 55, 66, 40, 57, 66, …
$ Smoke         <chr> "No", "No", "No", "No", "No", "No", "No", "No", "No", "N…
$ Quetelet      <dbl> 21.4838, 23.8763, 20.0108, 25.1406, 20.9850, 27.5214, 22…
$ Vitamin       <int> 1, 1, 2, 3, 1, 3, 2, 1, 3, 3, 1, 2, 3, 1, 3, 3, 1, 1, 3,…
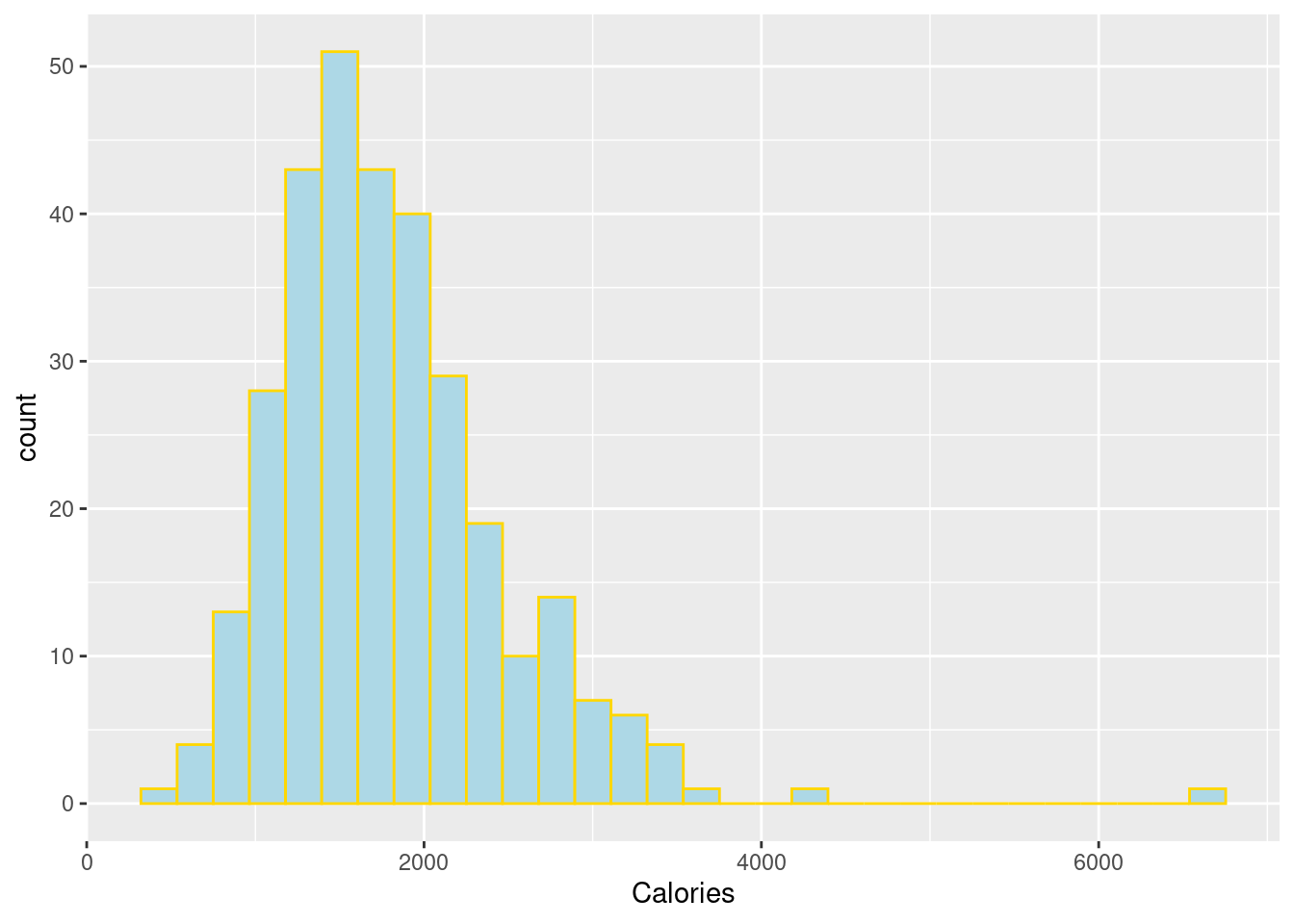
$ Calories      <dbl> 1298.8, 1032.5, 2372.3, 2449.5, 1952.1, 1366.9, 2213.9, …
$ Fat           <dbl> 57.0, 50.1, 83.6, 97.5, 82.6, 56.0, 52.0, 63.4, 57.8, 39…
$ Fiber         <dbl> 6.3, 15.8, 19.1, 26.5, 16.2, 9.6, 28.7, 10.9, 20.3, 15.5…
$ Alcohol       <dbl> 0.0, 0.0, 14.1, 0.5, 0.0, 1.3, 0.0, 0.0, 0.6, 0.0, 1.0, …
$ Cholesterol   <dbl> 170.3, 75.8, 257.9, 332.6, 170.8, 154.6, 255.1, 214.1, 2…
$ BetaDiet      <int> 1945, 2653, 6321, 1061, 2863, 1729, 5371, 823, 2895, 330…
$ RetinolDiet   <int> 890, 451, 660, 864, 1209, 1439, 802, 2571, 944, 493, 535…
$ BetaPlasma    <int> 200, 124, 328, 153, 92, 148, 258, 64, 218, 81, 184, 91, …
$ RetinolPlasma <int> 915, 727, 721, 615, 799, 654, 834, 825, 517, 562, 935, 7…
$ Gender        <chr> "Female", "Female", "Female", "Female", "Female", "Femal…
$ VitaminUse    <chr> "Regular", "Regular", "Occasional", "No", "Regular", "No…
$ PriorSmoke    <int> 2, 1, 2, 2, 1, 2, 1, 1, 1, 2, 2, 1, 1, 1, 1, 2, 2, 2, 1,…

(a) EDA

Always plot your data and get summary stats:

library(ggplot2)
ggplot(NutritionStudy, aes(Calories)) + geom_histogram(fill = "lightblue", color = "gold")

mean(NutritionStudy$Calories)

[1] 1796.655

sd(NutritionStudy$Calories)

[1] 680.3474

(b) SE for the sample mean

What is the estimated SE for the sample mean?

Click for answer

Answer:

n <- length(NutritionStudy$Calories)
SE <- sd(NutritionStudy$Calories) / sqrt(n)
SE

[1] 38.33324

(c) t-test statistic

Compute the t-test statistic for testing if the population mean calorie intake is equal, or not, to 2000.

Click for answer

Answer:

t_stat <- (mean(NutritionStudy$Calories) - 2000) / SE
t_stat

[1] -5.304676

(d) One-sample t-test

Perform a one-sample t-test to test whether the population mean calorie intake is equal to 2000 or not.

Click for answer

Answer:

t.test(NutritionStudy$Calories, mu = 2000)


    One Sample t-test

data:  NutritionStudy$Calories
t = -5.3047, df = 314, p-value = 2.135e-07
alternative hypothesis: true mean is not equal to 2000
95 percent confidence interval:
 1721.232 1872.077
sample estimates:
mean of x 
 1796.655

(e) One-sample t confidence interval

What is the 95% confidence interval for the population mean calorie intake?

Click for answer

Answer:

ci <- t.test(NutritionStudy$Calories, mu = 2000)$conf.int
ci

[1] 1721.232 1872.077
attr(,"conf.level")
[1] 0.95

(f) `qt` and `pt`

Show how to compute the p-value for the test in (d) using the pt command. Then show how the confidence interval in (e) is computed with a qt value.

Click for answer

Answer:

p_value <- 2 * pt(-abs(t_stat), df = n - 1)
p_value

[1] 2.135134e-07

t_star <- qt(0.975, df = n - 1)
t_star

[1] 1.967548

Practice Problems 19

Problem 1: Florida Lakes pH

(a) EDA

(b) SE for the sample mean

(c) t-test statistic

(d) One-sample t-test

(e) One-sample t confidence interval

(f) qt and pt

Problem 2: Nutrition Study

(a) EDA

(b) SE for the sample mean

(c) t-test statistic

(d) One-sample t-test

(e) One-sample t confidence interval

(f) qt and pt

(f) `qt` and `pt`

(f) `qt` and `pt`