p.hat <- 1329/2253
p.hat[1] 0.5898802Practice Problems 7
Problem 1: Using Search Engines on the Internet
A 2012 survey of a random sample of 2253 US adults found that 1,329 of them reported using a search engine (such as Google) every day to find information on the Internet.
a). Find the relevant proportion and give the correct notation with it.
Click for answer
Answer: \(\hat{p} = 1329/2253\)
b). Is your answer to part (a) a parameter or a statistic?
Click for answer
Answer: Statistic
c). Give notation for and define the population parameter that we estimate using the result of part (a).
Click for answer
Answer: p = the proportion of all US adults that would report that they use an Internet search engine every day
Problem 2: Bootstrapping mean
Let’s visualize the distribution of the sample mean. The following is a vector X containing the \(6\) data points:
X <- c(20, 24, 19, 23, 22, 16) # our dataWe start by creating 500 bootstrap samples from our data. Bootstrapping is a resampling technique where we sample with replacement from the original data, usually the same number of observations as the original dataset, to create ‘new’ samples. This process mimics the sampling variability inherent in collecting data. For each bootstrap sample, we calculate the mean.
bootstrapped_means <- sapply(1:500, function(i) mean(sample(X, replace = TRUE)))
# Or using replicate which is more concise for this case:
bootstrapped_means <- replicate(500, mean(sample(X, replace = TRUE)))
# To get a data frame similar to the tibble you created with purrr:
bootstrapped_means_df <- data.frame(
iteration = 1:500,
mean = bootstrapped_means
)After calculating the bootstrap sample means, we visualize their distribution using a dot plot. This plot will give us a sense of the sampling distribution of the mean - showing us where the mean is most likely to fall and how much it can vary.
library(ggplot2)
ggplot(bootstrapped_means_df, aes(x = mean)) +
geom_dotplot(dotsize = 0.7,
stackratio = 0.9,
binwidth = .13,
color = "gold",
fill = "blue") +
ggtitle("") + xlab("") + ylab("") +
scale_x_continuous(limits = c(17, 24),
expand = c(0, 0),
breaks = seq(17, 24, 1)) +
labs(title = "Bootstrap distribution of sample mean")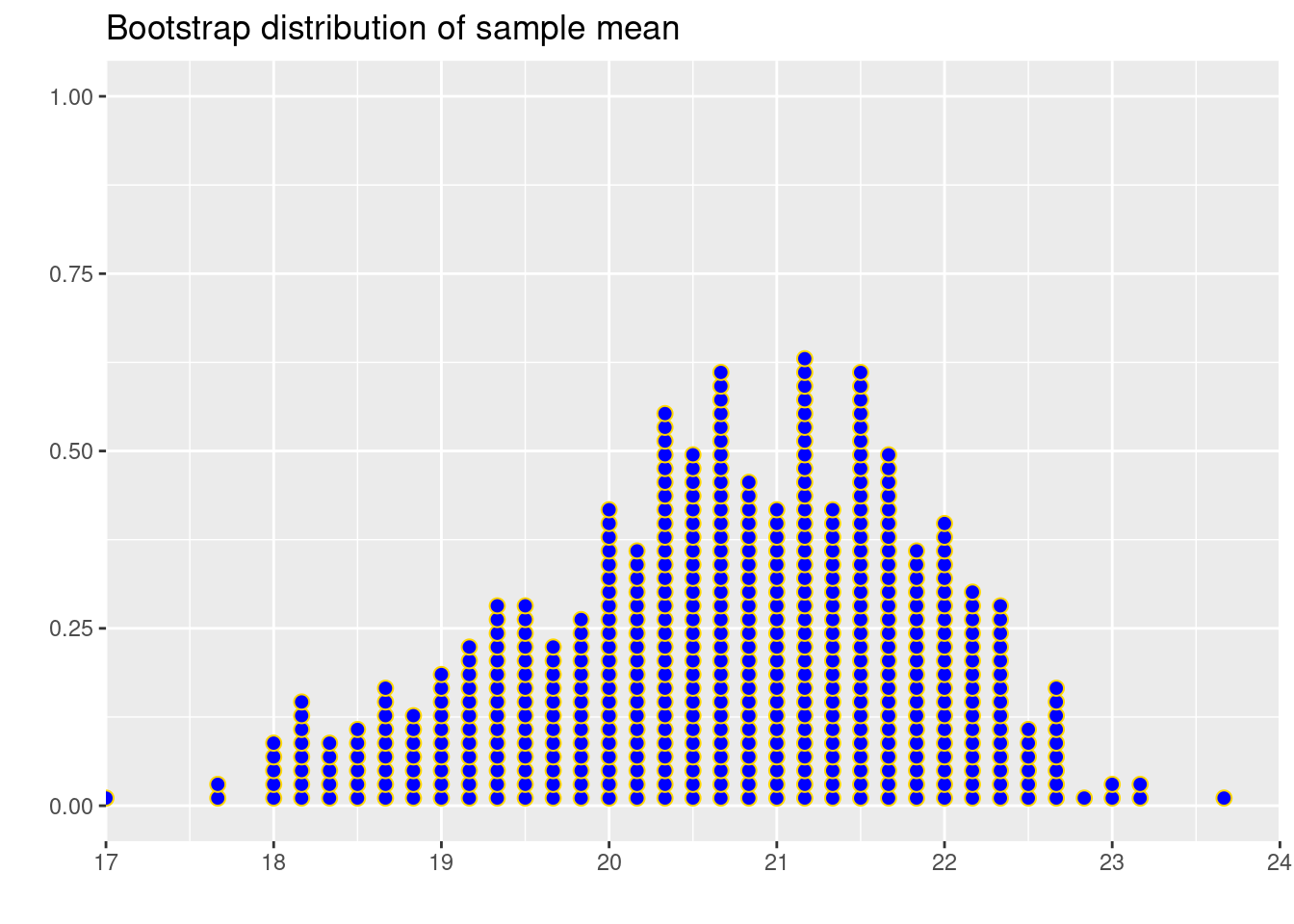
Click for answer
Answer: One sample mean from the bootstrapped sample.
Question: What is the shape of your sampling distribution?
Click for answer
Answer: Roughly symmetric.
Question: Where is your distribution centered?
Click for answer
Answer: About 20.5
Click for answer
Answer: It is close to the original sample mean. We do not know the population mean, so the bootstrap distribution will carry the bias of the original sample mean.
Question: What is the standard deviation of this distribution? (Hint: use the 95% rule.)
Click for answer
Answer: About 1.25, it looks like most of the bootstrapped sample means are between 18 to 23 so 2 standard deviations is about 2.5. This makes the SD about 1.25.
Question: The standard deviation of sampling distribution has a separate name. It is called the Standard Error. The standard deviation of this distribution is 1.1651075.
Click for answer
Answer: It’s close.
Problem 3: Simulation of a Sample Proportion
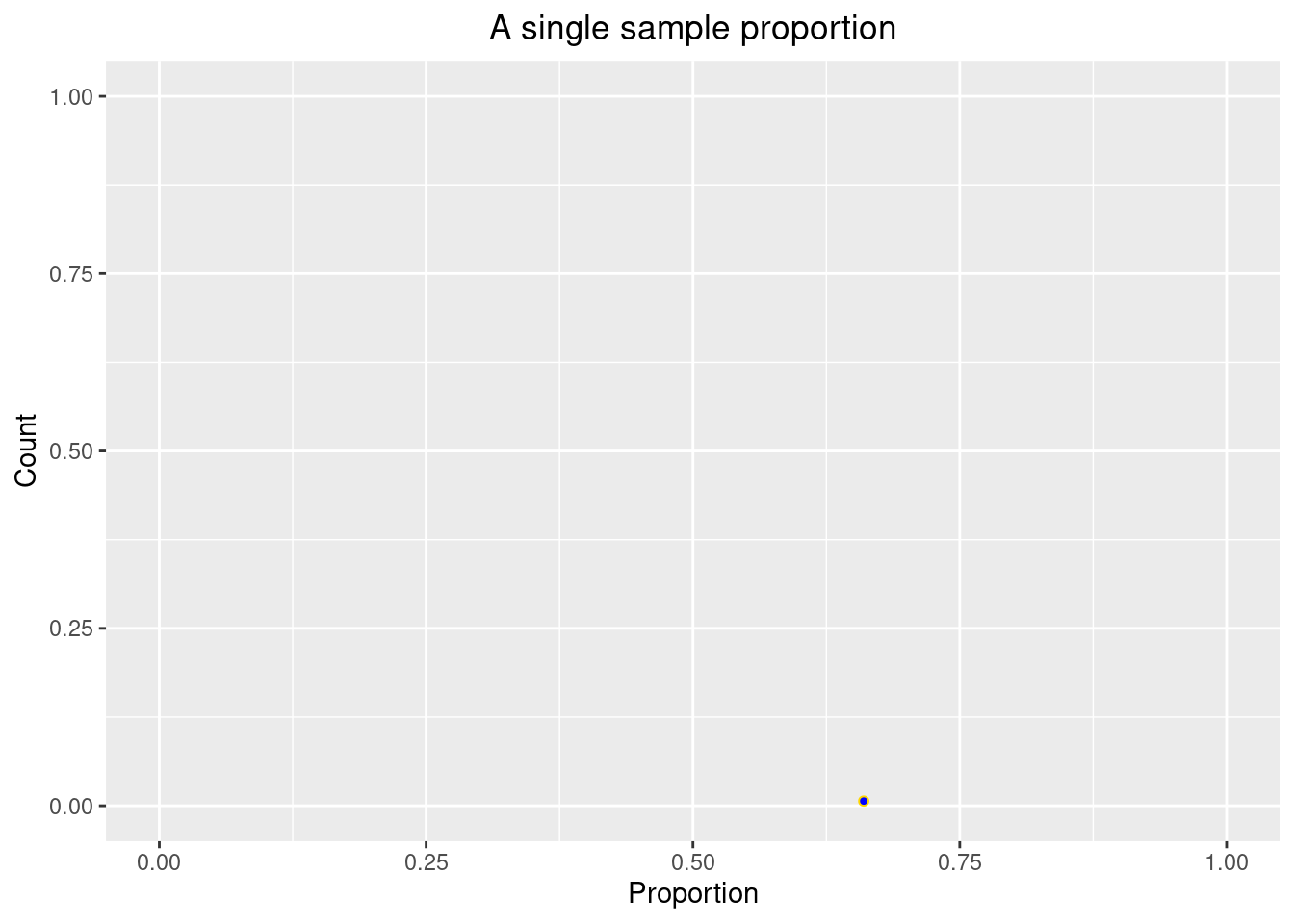
According to a PEW survey, \(66\%\) of U.S. adult citizens casted a ballot in the 2020 election. Suppose we take a random sample of \(n=100\) eligible U.S. voters and computed the sample proportion who voted.
# Define parameters
pop.prop <- .66 # Population proportion
n.size <- 100 # sample sizeLet’s plot this sample proportion in R.
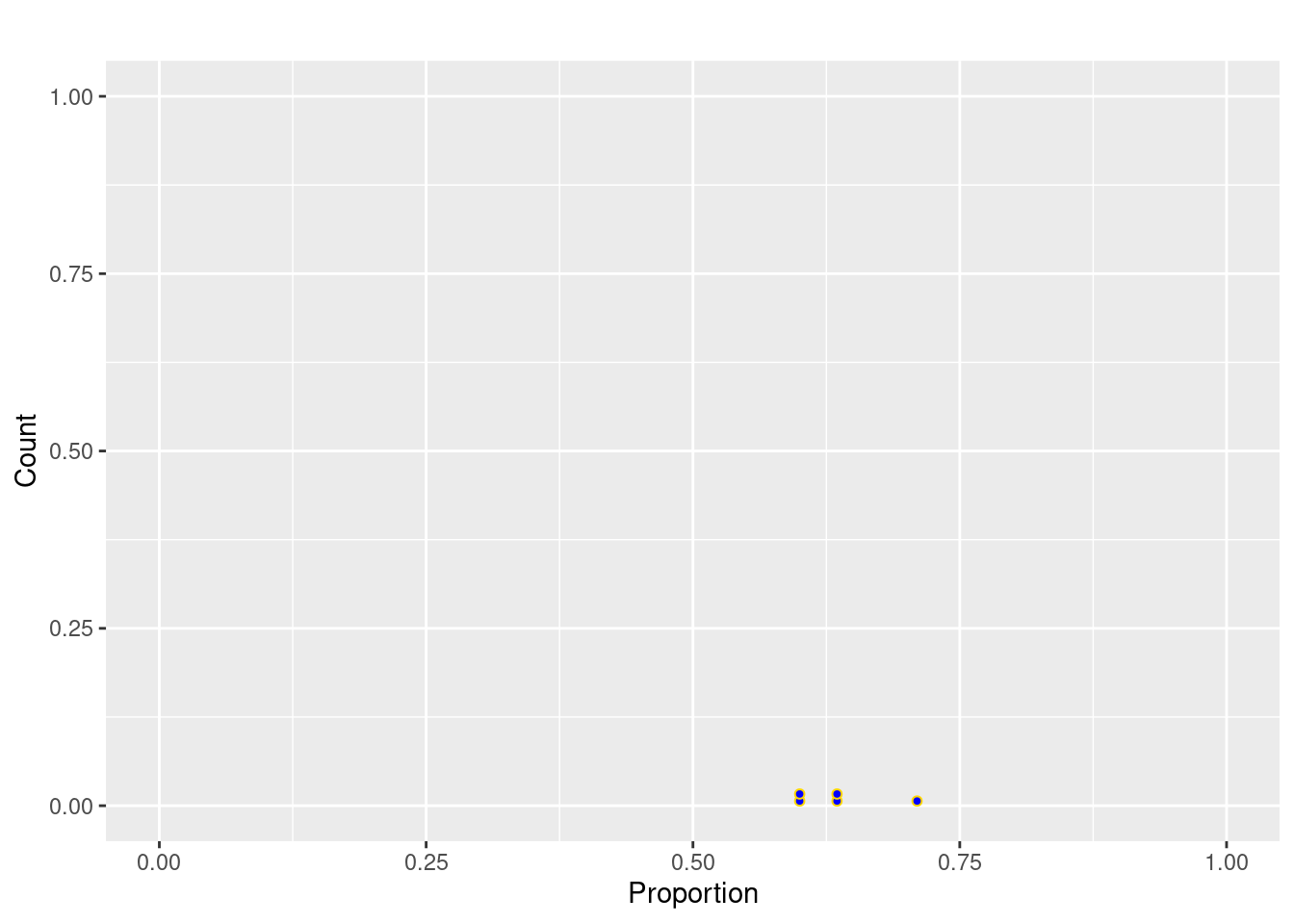
Similarly, we can generate 5 random samples of size \(n= 100\) and plot the sample proportions.
Continuing on, we can generate 500 random samples of size \(n= 100\) and plot the sample proportions.
Click for answer
Answer: One sample proportion from a sample of n=100 eligible voters.
Question: What is the shape of your sampling distribution?
Click for answer
Answer: Roughly symmetric.
Question: Where is your distribution centered?
Click for answer
Answer: About 0.66, which is the population proportion.
Question: The distribution should be centered at the population proportion. Verify that the distribution is centered around the population proportion, \(p = 0.66\). The mean of the sampling distribution of the proportion is 0.66298.
Click for answer
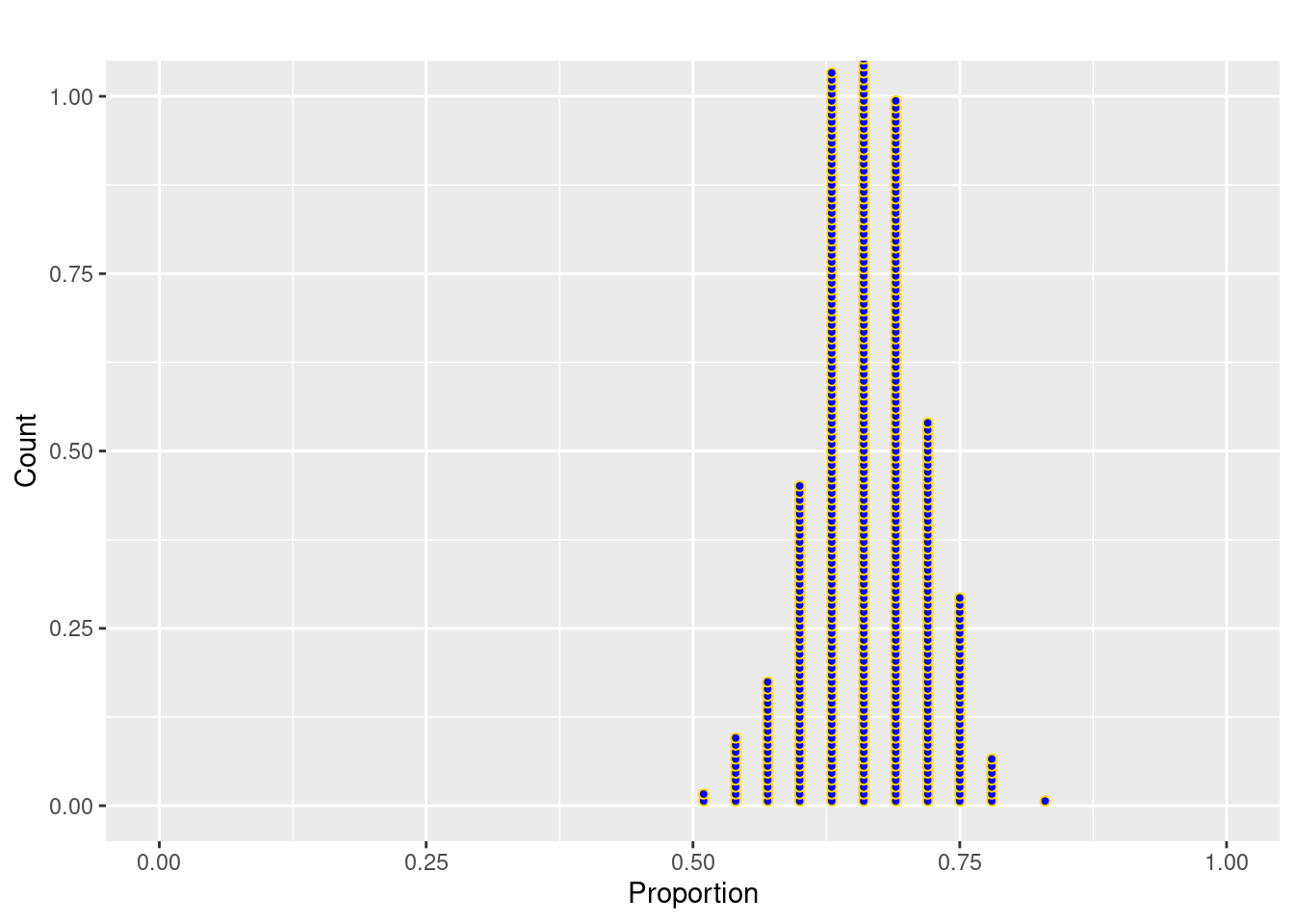
Answer: The center of the distribution is close to 0.66.
mean(sample.prop500)[1] 0.66298
Click for answer
Answer: About 0.05, it looks like most sample proportions are between 0.55 to 0.75 so 2 standard deviations is about 0.10. This makes the SD about 0.05.
Question: The standard deviation of sampling distribution has a separate name. It is called the Standard Error. The standard deviation of this distribution is 0.0494673.
Click for answer
Answer: The standard error is close.
(d) Now, let’s repeat part(c) with sample size 20 instead of 100 by generating and plotting 500 sample proportions.
Click for answer
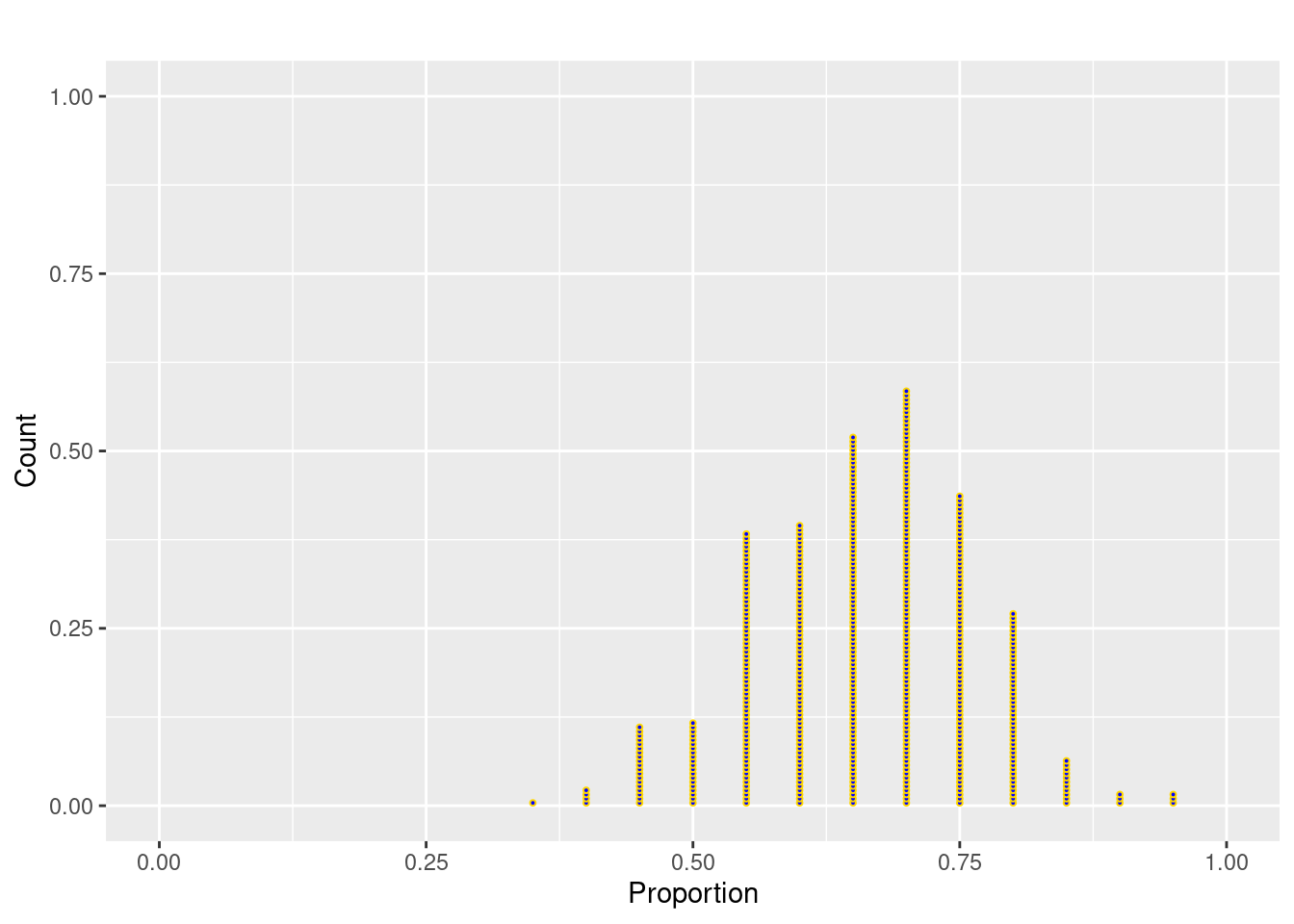
Answer: The shape is slightly left skewed, still centered at 0.66 but with more variability that before (SD of about 0.10). This distribution is more discrete looking because there are just a few sample proportions possible with n=20 (e.g. 20/20, 19/20, 18/20, etc).
mean(sample.prop500_size10)[1] 0.6603sd(sample.prop500_size10)[1] 0.1024202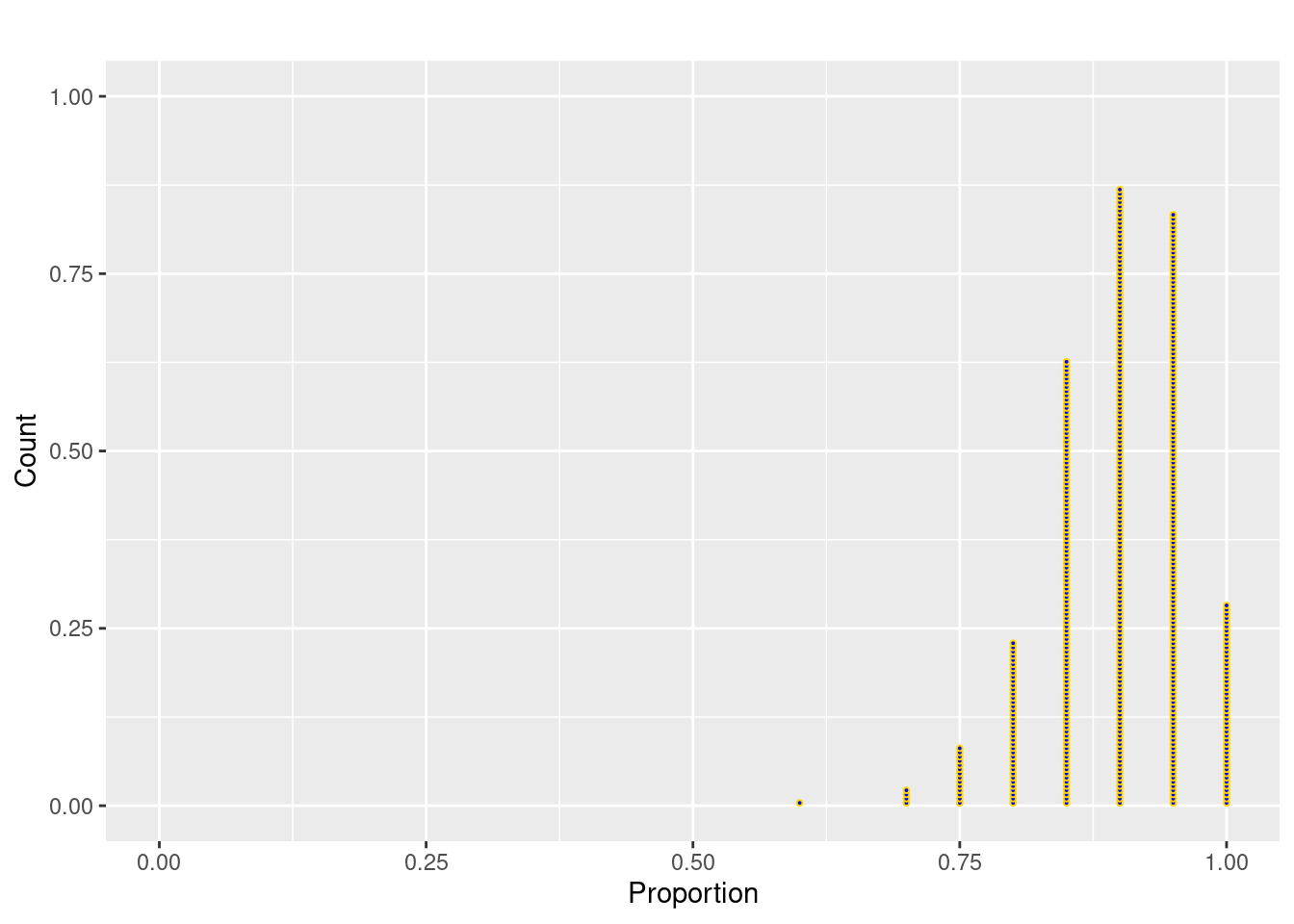(d) Now suppose the population proportion is \(p=0.90\) instead of \(p=0.66\) in part (e). Keep n=20.
Click for answer
Answer: The shape is much more left skewed than when p=0.66. Center is around 0.90 and SD is around 0.07. Note that increasing the population proportion closer to 1 results in a decrease in the SD because most samples give proportion near 1.
mean(sample.prop500_size10_large_p)[1] 0.8989sd(sample.prop500_size10_large_p)[1] 0.06412499